第43题
已知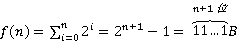
，计算f(n)的C语言函数f1如下：
1 2 3 4 5 6 7 8 | int f1(unsigned n){
int sum=1, power=1;
for(unsigned i=0;i<=n-1;i++){
power *= 2;
sum += power;
}
return sum;
}
|
将f1中的int都改为float，可得到计算f(n)的另一个函数f2。假设unsigned和int型数据都占32位，float采用IEEE754单精度标准。请回答下列问题。
（1）当n=0时，f1会出现死循环，为什么？若将f1中的变量和n都定义为int型，则f1是否还会出现死循环？为什么？
（2）f1(23)和f2(23)的返回值是否相等？机器数各是什么(用十六进制表示)？
（3）f1(24)和f2(24)的返回值分别为33 554 431和33 554 432.0，为什么不相等？
（4）f(31)=232-1，而f1(31)的返回值却为-1，为什么？若使f1(n)的返回值与f(n)相等，则最大的n是多少？
（5）f2(127)的机器数为7F80 0000H，对应的值是什么？若使f2(n)的结果不溢出，则最大的n是多少？若使f2(n)的结果精确(无舍入)。则最大的n是多少？
答：
（1）由于i和n是unsigned型，故“i<=n-1”是无符号数比较，n=0时，n-1的机器数为全1，值是232-1，为unsigned型可表示的最大数，条件“i<=n-1”永真，因此出现死循环。(2分)
若i和n改为int类型，则不会出现死循环。(1分)
因为“i<=n-1”是带符号整数比较，n=0时，n-1的值是-1，当i=0时条件“i<=n-1”不成立，此时退出for循环。(1分)
（2）f1(23)与f2(23)的返回值相等。（1分）f(23) = 223+1-1 = 224-1，它的二进制形式是24个1。int占32位，没有溢出。float有1个符号位，8个指数位，23个底数位，23个底数位可以表示24位的底数。所以两者返回值相等。
f1(23)的机器数是 00FF FFFFH。（1分）
f2(23)的机器数是 4B7F FFFFH。（1分）
显而易见前者是24个1，即 0000 0000 1111 1111 1111 1111 1111 1111（2），后者符号位是 0，指数位为 23+127(10) = 1001 0110（2），底数位是 111 1111 1111 1111 1111 1111（2）。
（3）当n=24时，f(24) = 1 1111 1111 1111 1111 1111 1111 B，而float型数只有24位有效位，舍入后数值增大，所以f2(24)比f1(24)大1。(1分)
（4）显然f(31)已超出了int型数据的表示范围，用f1(31)实现时得到的机器数为32个1，作为int型数解释时其值为-1，即f1(31)的返回值为-1。(1分)
因为int型最大可表示数是0后面加31个1，故使f1(n)的返回值与f(n)相等的最大n值是30。(1分)
（5）IEEE 754标准用“阶码全1、尾数全0”表示无穷大。f2返回值为float型，机器数7F80 0000H对应的值是+∞。(1分)当n=126时，f(126) = 2127-1 = 1.1…1×2126，对应阶码为127+126=253，尾数部分舍入后阶码加1，最终阶码为254，是IEEE 754单精度格式表示的最大阶码。故使f2结果不溢出的最大n值为126。(1分)当n=23时，f(23)为24位1，float型数有24位有效位，所以不需舍入，结果精确。故使f2获得精确结果的最大n值为23。(1分)