题目 2414:
信息学奥赛一本通T1506-最小圈
时间限制: 2s
内存限制: 192MB 提交: 6 解决: 5
题目描述
原题来自:HNOI 2009
考虑带权的有向图 G=(V,E) 以及 w:E→R,每条边e=(i,j)(i≠j,i∈V,j∈V)的权值定义为Wi,j,令 n=∣V|。c=(c1,c2,⋯,ck)(ci∈V) 是 G 中的一个圈当且仅当 (ci,ci+1)(1≤i<k) 和 (ck,c1) 都在 E 中,这时称 k 为圈 c 的长度。同时令 ck+1=c1 ,并定义圈 c=(c1,c2,⋯,ck) 的平均值为:
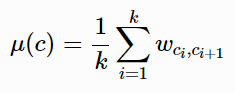
即 c 上所有边的权值的平均值。
令 μ∗(c)=min{μ(c)} 为 G 中所有圈 c 的平均值的最小值。现在的目标是:在给定了一个图 G=(V,E) 以及 w:E→R 之后,请求出 G 中所有圈 c 的平均值的最小值 μ∗(c)=min{μ(c)}。
考虑带权的有向图 G=(V,E) 以及 w:E→R,每条边e=(i,j)(i≠j,i∈V,j∈V)的权值定义为Wi,j,令 n=∣V|。c=(c1,c2,⋯,ck)(ci∈V) 是 G 中的一个圈当且仅当 (ci,ci+1)(1≤i<k) 和 (ck,c1) 都在 E 中,这时称 k 为圈 c 的长度。同时令 ck+1=c1 ,并定义圈 c=(c1,c2,⋯,ck) 的平均值为:
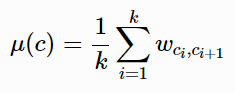
即 c 上所有边的权值的平均值。
令 μ∗(c)=min{μ(c)} 为 G 中所有圈 c 的平均值的最小值。现在的目标是:在给定了一个图 G=(V,E) 以及 w:E→R 之后,请求出 G 中所有圈 c 的平均值的最小值 μ∗(c)=min{μ(c)}。
输入格式
第一行包含两个正整数 n 和 m,并用一个空格隔开,其中 n=∣V∣,m=∣E∣,分别表示图中有 n 个顶点和 m 条边;
接下来 m 行,每行包含用空格隔开的三个数 i,j,wi,j ,表示有一条边 (i,j) 且该边的权值为 wi,j 。
输入数据保证图 G=(V,E) 连通,存在圈且有一个点能到达其他所有点。
接下来 m 行,每行包含用空格隔开的三个数 i,j,wi,j ,表示有一条边 (i,j) 且该边的权值为 wi,j 。
输入数据保证图 G=(V,E) 连通,存在圈且有一个点能到达其他所有点。
输出格式
仅包含一个实数 μ∗=min{μ(c)},要求输出到小数点后 8 位。
样例输入
4 5 1 2 5 2 3 5 3 1 5 2 4 3 4 1 3
样例输出
3.66666667
提示
数据范围:
对于 20% 的数据,1≤n≤100,1≤m≤1000;
对于 40% 的数据,1≤n≤1000,1≤m≤5000;
对于 100% 的数据,1≤n≤3000,1≤m≤104,∣wi,j∣≤107 。
输入保证 1≤i,j≤n。
对于 20% 的数据,1≤n≤100,1≤m≤1000;
对于 40% 的数据,1≤n≤1000,1≤m≤5000;
对于 100% 的数据,1≤n≤3000,1≤m≤104,∣wi,j∣≤107 。
输入保证 1≤i,j≤n。