题目 1949:
蓝桥杯算法提高VIP-House of Cards
时间限制: 2s
内存限制: 192MB 提交: 4 解决: 0
题目描述
Axel和Birgit喜欢玩这样的一种纸牌游戏:他们建造一个由纸牌组成的房子,当他们添加纸牌到房子的时候,会获得(或失去)游戏的分数。由于他们都有一双灵巧的手,纸牌组成的房子是不会倒塌的。他们使用半副标准纸牌。一副标准的纸牌有4种花色,2种是红色,2种是黑色。Axel和Birgit只使用2种花色,1红1黑。每种花色有13个等级。我们使用记号1R,2R,…,13R,1B,2B,…,13B来表示等级和颜色。
开始前,玩家要选择半副标准纸牌的一个子集,子集中所有纸牌的最大等级是M。洗完选出的纸牌后,他们从牌堆的最上面拿出8张,从左到右连续地放置它们形成4个“山峰”。举个例子,如果M=13而且前10张纸牌(26张的前10张)是:
6B 3R 5B 2B 1B 5R 13R 7B 11R 1R …
那么这个游戏开始的时候就像图7所展示的那样。
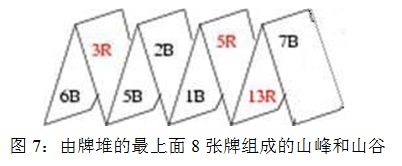
剩下的纸牌正面朝上被放置成一排。
每个玩家被认定一种颜色,红色或黑色。Birgit总被认定是黑色,Axel总被认定是红色。第一张用于组成山峰和山谷的纸牌的颜色决定了哪个玩家先开始。图7的那个例子,Birgit先开始,因为第一张纸牌是6B。
玩家交替进行操作。一步操作包括从一排纸牌的最前面抽取一张纸牌然后进行下列的一条:
1.持有这张纸牌直到下次操作(这是一张“被持有的纸牌”)。
2.用刚抽取的纸牌或被持有的纸牌覆盖在两个山峰之间的山谷,形成一个“基底”。如果还剩下一张牌,那么这张牌就被持有。
3.把2张纸牌放在基底上面,形成一个山峰(其中一张纸牌一定是一张被“持有”的纸牌)。
不是所有的选择总是可行的。任何时候最多持有1张纸牌,所以第一个选择只有当这个玩家没有持有纸牌时才可行。
因为排成一排的纸牌是正面朝上,所以两个玩家在纸牌被抽取前就事先知道纸牌的顺序。
如果玩家通过添加了一个基底组成了一个向下的三角形,或者通过添加了一个山峰组成了一个向上的三角形,那么玩家的分数就会像下面描述的那样更新。组成三角形的3张纸牌的等级之和将被增加到那个颜色与3张纸牌的多数颜色相等的那个玩家的分数上。如果在游戏中没有组成三角形,两个玩家的分数保持不变。
图7的那个例子,如果Birgit放置她的纸牌(11R)到中间的山谷上,她将获得14分。如果她放置她的纸牌到左边的山谷上,Axel获得19分。如果她放置她的纸牌到右边的山谷上,Axel获得29分。
如果在某步操作结束后没有纸牌等待被抽取,这个游戏就结束了。如果某个玩家在这个时候持有纸牌,那个玩家的分数将会增加(或减少)这张纸牌的等级如果这张纸牌的颜色与玩家颜色相同(不同)。
当这个游戏结束后,分数低的玩家将要支付一定数量的瑞典克朗给另一个玩家,数量等同于两个玩家的分数差。如果是平局,就不用支付。
你必须写一个程序读入一副被洗过的牌堆和一个玩家的名字,然后找出这个玩家最多能赢多少(或者最少能输多少),假设另一个玩家总是采取最优策略。
开始前,玩家要选择半副标准纸牌的一个子集,子集中所有纸牌的最大等级是M。洗完选出的纸牌后,他们从牌堆的最上面拿出8张,从左到右连续地放置它们形成4个“山峰”。举个例子,如果M=13而且前10张纸牌(26张的前10张)是:
6B 3R 5B 2B 1B 5R 13R 7B 11R 1R …
那么这个游戏开始的时候就像图7所展示的那样。
剩下的纸牌正面朝上被放置成一排。
每个玩家被认定一种颜色,红色或黑色。Birgit总被认定是黑色,Axel总被认定是红色。第一张用于组成山峰和山谷的纸牌的颜色决定了哪个玩家先开始。图7的那个例子,Birgit先开始,因为第一张纸牌是6B。
玩家交替进行操作。一步操作包括从一排纸牌的最前面抽取一张纸牌然后进行下列的一条:
1.持有这张纸牌直到下次操作(这是一张“被持有的纸牌”)。
2.用刚抽取的纸牌或被持有的纸牌覆盖在两个山峰之间的山谷,形成一个“基底”。如果还剩下一张牌,那么这张牌就被持有。
3.把2张纸牌放在基底上面,形成一个山峰(其中一张纸牌一定是一张被“持有”的纸牌)。
不是所有的选择总是可行的。任何时候最多持有1张纸牌,所以第一个选择只有当这个玩家没有持有纸牌时才可行。
因为排成一排的纸牌是正面朝上,所以两个玩家在纸牌被抽取前就事先知道纸牌的顺序。
如果玩家通过添加了一个基底组成了一个向下的三角形,或者通过添加了一个山峰组成了一个向上的三角形,那么玩家的分数就会像下面描述的那样更新。组成三角形的3张纸牌的等级之和将被增加到那个颜色与3张纸牌的多数颜色相等的那个玩家的分数上。如果在游戏中没有组成三角形,两个玩家的分数保持不变。
图7的那个例子,如果Birgit放置她的纸牌(11R)到中间的山谷上,她将获得14分。如果她放置她的纸牌到左边的山谷上,Axel获得19分。如果她放置她的纸牌到右边的山谷上,Axel获得29分。
如果在某步操作结束后没有纸牌等待被抽取,这个游戏就结束了。如果某个玩家在这个时候持有纸牌,那个玩家的分数将会增加(或减少)这张纸牌的等级如果这张纸牌的颜色与玩家颜色相同(不同)。
当这个游戏结束后,分数低的玩家将要支付一定数量的瑞典克朗给另一个玩家,数量等同于两个玩家的分数差。如果是平局,就不用支付。
你必须写一个程序读入一副被洗过的牌堆和一个玩家的名字,然后找出这个玩家最多能赢多少(或者最少能输多少),假设另一个玩家总是采取最优策略。
输入格式
读入包含多组测试数据代表多个游戏。每组测试数据包含一个名字(Axel或者Birgit),然后会有1个最大的等级M(5 ≤ M ≤ 13),紧接着有2M张纸牌的等级和颜色,按在牌堆中的位置给出。每一个等级(从1到M)和颜色的组合在序列中只会出现一次。初始序列的前8张按抽出的顺序从左到右组成山峰,剩下的显示了纸牌的顺序。
包含单词End的一行紧跟在最后一组数据后面。
包含单词End的一行紧跟在最后一组数据后面。
输出格式
对于每个测试数据,输出数据的编号(从1开始),这组数据中玩家的名字,和这个玩家赢或输了多少分数。如果是平局,指出是平局而不是输出数字。参照样例输出的格式。
样例输入
Axel 5 1R 2R 3R 4R 5R 5B 4B 3B 2B 1B Birgit 5 1R 2R 3R 4R 5R 5B 4B 3B 2B 1B Birgit 5 1R 1B 3R 4R 5R 5B 4B 3B 2R 2B End
样例输出
Case 1: Axel wins 1 Case 2: Birgit loses 1 Case 3: Axel and Birgit tie