凸包(Convex Hull)是一个计算几何(图形学)中的概念。
在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。
X的凸包可以用X内所有点(X1,...Xn)的线性组合来构造.
在二维欧几里得空间中,凸包可想象为一条刚好包著所有点的橡皮圈。
用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有的点。
例子:假设平面上有p0~p12共13个点,过某些点作一个多边形,使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候,我们就叫它“凸包”。如下图:
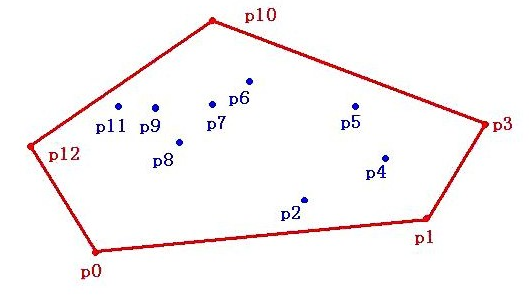
一、二维凸包
1. 定义
凸多边形是指所有内角大小都在[0,π]范围内的简单多边形。
在平面上能包含所有给定点的最小凸多边形叫做凸包。
其定义为:对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。
实际上可以理解为用一个橡皮筋包含住所有给定点的形态。
凸包用最小的周长围住了给定的所有点。如果一个凹多边形围住了所有的点,它的周长一定不是最小,如下图。根据三角不等式,凸多边形在周长上一定是最优的。

2. Andrew 算法求凸包
常用的求法有 Graham 扫描法和 Andrew 算法,这里主要介绍 Andrew 算法。
(1)性质
该算法的时间复杂度为O(nlogn),其中 n 为待求凸包点集的大小,同时复杂度的瓶颈也在于对所有点坐标的双关键字排序。
(2)过程
首先把所有点以横坐标为第一关键字,纵坐标为第二关键字排序。
显然排序后最小的元素和最大的元素一定在凸包上。而且因为是凸多边形,我们如果从一个点出发逆时针走,轨迹总是“左拐”的,一旦出现右拐,就说明这一段不在凸包上。因此我们可以用一个单调栈来维护上下凸壳。
因为从左向右看,上下凸壳所旋转的方向不同,为了让单调栈起作用,我们首先升序枚举求出下凸壳,然后降序求出上凸壳。
求凸壳时,一旦发现即将进栈的点(P)和栈顶的两个点(S1,S2,其中S1为栈顶)行进的方向向右旋转,即叉积小于0:![]() ,则弹出栈顶,回到上一步,继续检测,直到
,则弹出栈顶,回到上一步,继续检测,直到![]() 或者栈内仅剩一个元素为止。
或者栈内仅剩一个元素为止。
通常情况下不需要保留位于凸包边上的点,因此上面一段中![]() 这个条件中的“<”可以视情况改为≤,同时后面一个条件应改为>。
这个条件中的“<”可以视情况改为≤,同时后面一个条件应改为>。
(3)实现:
// C++ Version
// stk[] 是整型,存的是下标
// p[] 存储向量或点
tp = 0; // 初始化栈
std::sort(p + 1, p + 1 + n); // 对点进行排序
stk[++tp] = 1;
// 栈内添加第一个元素,且不更新 used,使得 1 在最后封闭凸包时也对单调栈更新
for (int i = 2; i <= n; ++i) {
while (tp >= 2 // 下一行 * 操作符被重载为叉积
&& (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)
used[stk[tp--]] = 0;
used[i] = 1; // used 表示在凸壳上
stk[++tp] = i;
}
int tmp = tp; // tmp 表示下凸壳大小
for (int i = n - 1; i > 0; --i)
if (!used[i]) {
// ↓求上凸壳时不影响下凸壳
while (tp > tmp && (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)
used[stk[tp--]] = 0;
used[i] = 1;
stk[++tp] = i;
}
for (int i = 1; i <= tp; ++i) // 复制到新数组中去
h[i] = p[stk[i]];
int ans = tp - 1;# Python Version stk = [] # 是整型,存的是下标 p = [] # 存储向量或点 tp = 0 # 初始化栈 p.sort() # 对点进行排序 stk[tp] = 1 tp = tp + 1 # 栈内添加第一个元素,且不更新 used,使得 1 在最后封闭凸包时也对单调栈更新 for i in range(2, n + 1): while tp >= 2 and (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0: # 下一行 * 操作符被重载为叉积 used[stk[tp]] = 0 tp = tp - 1 used[i] = 1 # used 表示在凸壳上 stk[tp] = i tp = tp + 1 tmp = tp # tmp 表示下凸壳大小 for i in range(n - 1, 0, -1): if used[i] == False: # ↓求上凸壳时不影响下凸壳 while tp > tmp and (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0: used[stk[tp]] = 0 tp = tp - 1 used[i] = 1 stk[tp] = i tp = tp + 1 for i in range(1, tp + 1): h[i] = p[stk[i]] ans = tp - 1
根据上面的代码,最后凸包上有ans个元素(额外存储了1号点,因此 h 数组中有 ans+1 个元素),并且按逆时针方向排序。周长就是
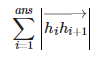
二、三维凸包
圆的反演:反演中心为O,反演半径为R,若经过O的直线经过P,P′,且OPXP′=R^2,则称P、P′关于 O 互为反演。
求凸包的过程如下:
(1)首先对其微小扰动,避免出现四点共面的情况。
(2)对于一个已知凸包,新增一个点 P,将 P 视作一个点光源,向凸包做射线,可以知道,光线的可见面和不可见面一定是由若干条棱隔开的。
(3)将光的可见面删去,并新增由其分割棱与 P 构成的平面。重复此过程即可,由Pick定理、欧拉公式(在凸多面体中,其顶点 V、边数 E 及面数 F 满足 V-E+F=2)和圆的反演,复杂度![]() 。
。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程