归并排序算法是在分治算法基础上设计出来的一种排序算法,它可以对指定序列完成升序(由小到大)或降序(由大到小)排序,对应的时间复杂度为O(nlogn)。
(1)算法思路
归并排序算法实现排序的思路是:
1. 将整个待排序序列划分成多个不可再分的子序列,每个子序列中仅有 1 个元素;
2. 所有的子序列进行两两合并,合并过程中完成排序操作,最终合并得到的新序列就是有序序列。
(2)动图演示
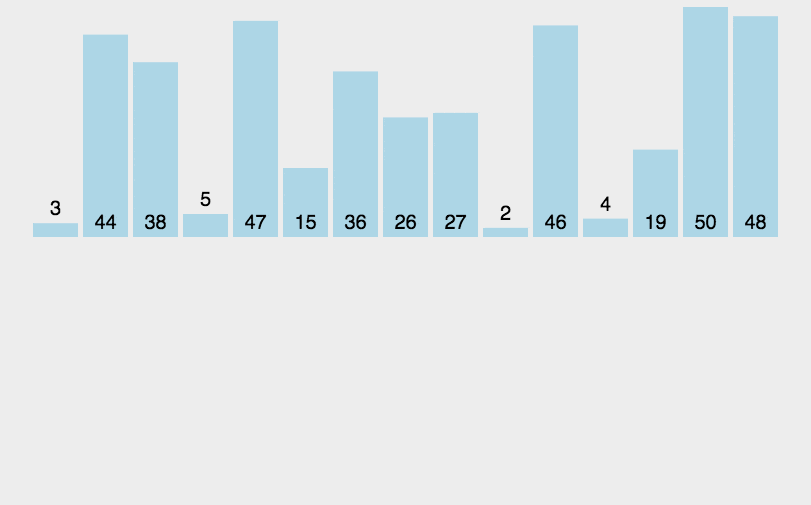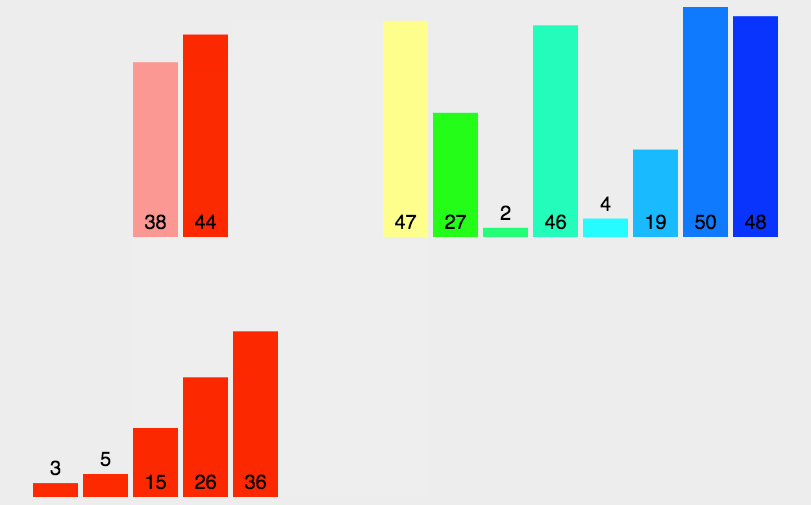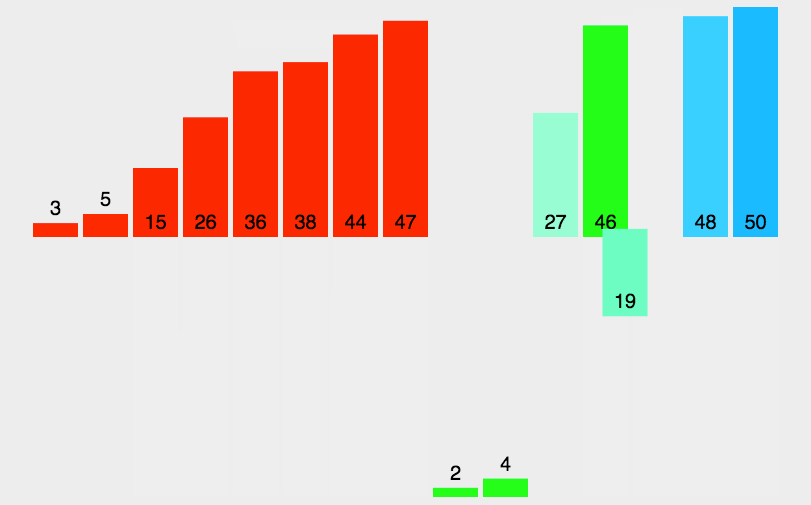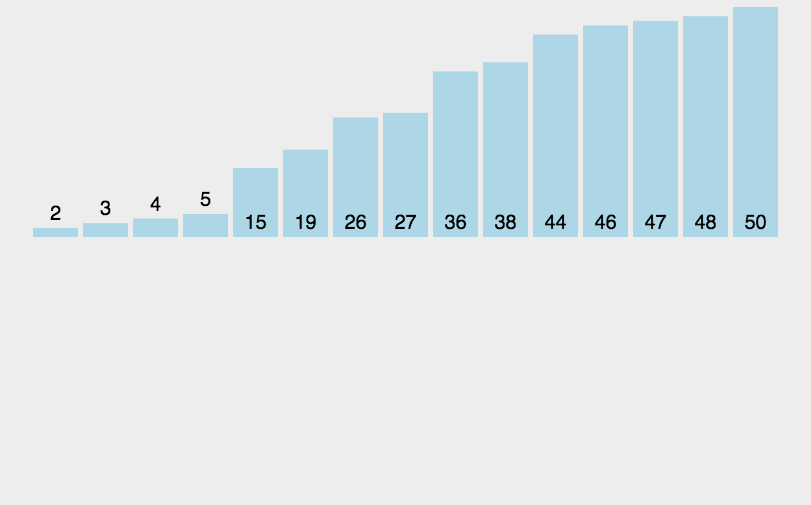
(3)归并排序的特性总结:
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
(4)C语言代码实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 | #include<stdio.h>#include<stdlib.h>void Merge(int arr[], int tmp[], int start,int mid, int end)//合并小组并排序{ int i = start;//i标识//左小组的第一个元素位置 int j = mid + 1;//j标识//右小组的第一个元素位置 int k = start;//tmp当前小组存放的起始位置 while (i < mid + 1 && j < end + 1)//左小组越界或右小组越界才能退出 { if (arr[i] <= arr[j]) { tmp[k++] = arr[i++]; } else { tmp[k++] = arr[j++]; } } while (j < end + 1)//如果右边小组没有越界 { tmp[k++] = arr[j++]; } while (i < mid + 1)//如果左边小组没有越界 { tmp[k++] = arr[i++]; }//哦哦就是补齐了,把数组放到新的那个临时数组中去了 for (i = start; i <= end; i++) { arr[i] = tmp[i]; }//至此,原来的数组已经排序完毕}void MergeS(int arr[], int tmp[], int start, int end)//划分小组,现在没有end.{ if (start < end) { int mid = (start+end)/2; MergeS(arr, tmp, start, mid); MergeS(arr, tmp, mid + 1, end);//自我递归调用 Merge(arr, tmp, start, mid, end);//现在就全部排号 }}//就是递归调用呗void MergeSort(int arr[], int len){ int *tmp = (int *)malloc(sizeof(int)*len);//开了一个排序后结果保存的临时数组 MergeS(arr, tmp, 0, len - 1);//嵌套调用 free(tmp);}int main(){ int arr[] = { 12, 3, 21, 32, 1, 34, 12, 35, 34 };//举例子 //int s,arr[100]; //scanf("%d",&s); //for(int i=0;i<s;i++) //{ // scanf("%d ",&arr[i]); //} int len = sizeof(arr) / sizeof(arr[0]); MergeSort(arr, len); for (int i = 0; i < len; i++) { printf("%d ", arr[i]); } printf("\n"); return 0;} |
如果我们编译并运行上述程序,那么它应该产生以下结果:
1 | 1 3 12 12 21 32 34 34 35 |
| 1719 | 数据结构-归并排序 |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程