前缀和理解与应用

本篇内容主要学习前缀和与其应用。

一、前缀和概念

前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化。

简单来说：我们有一个数组x和它的前缀和数组y，他们满足以下公式。

y 0 = x 0

y 1 = x 0 + x 1

y 2 = x 0 + x 1 + x 2

...

即 y[n]=x[1]+x[2]+...+x[n]。

二、前缀和分为一维前缀和二维前缀和

（1）一维前缀和

一维前缀和的得到很简单，也很好理解，我们只需要遍历的时候一直把之前计算的和 加上自己就能得到当前的和。

for (i=1; i<=n; i++) {
    cin >> a[i];
    s[i] = s[i-1] + a[i];
}

（2）二维前缀和

先上一张图，看图就知道是个什么逻辑了。

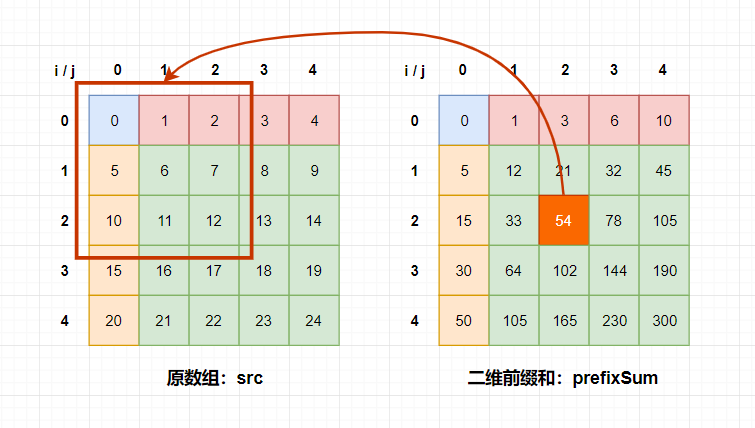
前缀和数组里每一个位置都表示原数组当前index左上方的数字的和。

比如像图里面画的：prefixSum[3, 3] = src[0~2, 0~2]的和;

二维前缀和数组要怎么计算出来呢？

可以分为四种情况

1. i==0 && j==0，只有一个直接赋值即可：prefixSum[0, 0] = src[0, 0]。

2. i==0，最左边的一排，图中黄色部分，prefixSum[0, j] = prefixSum[0, j-1] + src[0, j]；

3. j==0，最上面一排，途中红色部分，prefixSum[i, o] = prefixSum[i-1, 0] + src[i, 0];

4. i!=0 || j!=0，图中绿色部分，prefixSum[i][j] = prefixSum[i - 1][j] + prefixSum[i][j - 1] + src[i][j] - prefixSum[i - 1][j - 1];

具体讲第四步：

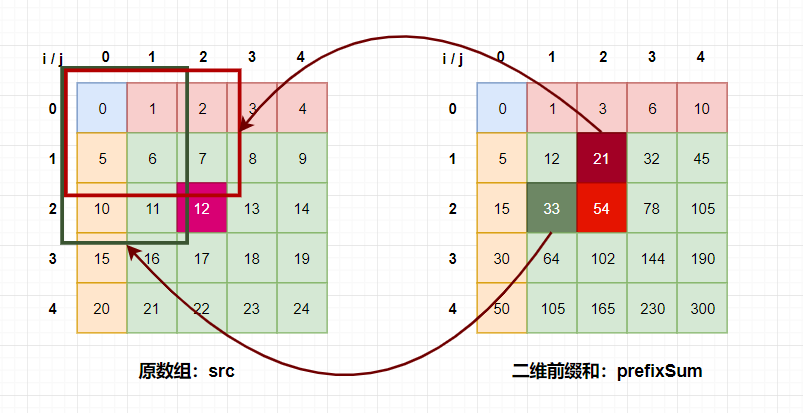
我们要得到prefixSum[2,2]，我们知道应该是图一中箭头指向的区域。也就是9个方框加起来的和，也就是54。

看图二，我们可以利用prefixSum[1, 2]和prefixSum[2, 1]，但是他俩的区域是重合的，如图二所示，重合的区域又恰好是prefixSum[1, 1]负责的区域，相当于加了两份，需要减掉一份。

所以prefixSum[2,2] = prefixSum[1, 2] + prefixSum[2, 1] - prefixSum[1, 1] + src[2, 2];

也就是54 = 33 + 21 -12(这个是prefixSum[1, 1]) +12(这是src[2, 2])

for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

三、前缀和的应用

例题：区间求和

给你一串长度为 n 的数列 a1, a2, a3, ..., an，再给出 m 个询问，每次询问给出 L, R 两个数，要求给出区间 [L, R] 里的数的和。

#include <iostream>
 
using namespace std;
 
const int MAXN = 1e5+2;
long long arr[MAXN] = {};
long long sum[MAXN] = {};
 
int main() {
    int n;
    cin >> n;
    
    int i, j;
    for (i=1; i<=n; i++) {
        cin >> arr[i];
        sum[i] = sum[i-1] + arr[i];
    }
 
    int m;
    int l, r;
    cin >> m;
    for (i=0; i<m; i++) {
        cin >> l >> r;
        cout << sum[r] - sum[l-1] << endl;
    }
 
    return 0;
}