回文树/回文自动机 (PAM) 实现及模板

咱们可以先从字面意思来理解什么是回文树，回文树 (回文自动机) 实际上是奇偶两棵树，每一个节点代表一个本质不同的回文子串（一棵树上的串长度全部是奇数，另一棵全部是偶数），原串中每一个本质不同的回文子串都在树上出现一次且仅一次。

一个节点的 fail 指针指向它的最长回文后缀（不包括自身，所有空 fail 均连向 1）。归纳容易证明，当在原串末尾新增一个字符时，回文树上至多会新增一个节点，这也证明了一个串本质不同的回文子串个数不会超过 n。

建树时采用增量构造法，当考虑新字符 s [i] 时，先找到以 s [i-1] 为结尾的节点 p，并不断跳 fail。若代表新增回文子串的节点已存在则直接结束，否则通过 fail [p] 不断跳 fail 找到新节点的 fail。

0,1 号节点均不代表串，常数大于 manacher。初始化 fail [0]=fail [1]=1,len [1]=-1,tot=1,last=0。

概述

回文自动机（简称PAM，又称回文树，Palindromic Tree）是一种用于处理回文串的结构，在其结构内可以找到原串中的所有回文子串，顾名思义，回文树是一个用来解决回文串相关问题的数据结构。

结构

就像线段树、平衡树等其它树结构一样，回文树由若干个节点组成，每个节点代表一个回文串(palindrome)。

如图为串abba的PAM示意图，其中，实线表示回文串的扩展转移边，虚线表示后缀链接。

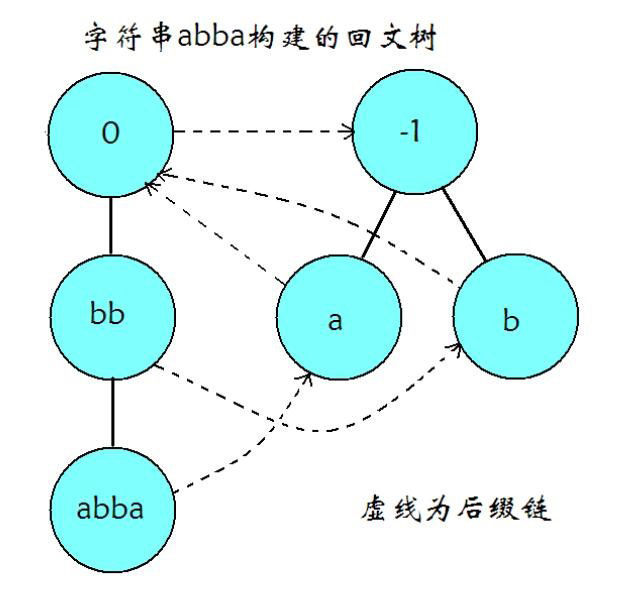
节点信息

每个节点对应一个唯一的回文子串。

（1）回文串出现的次数cnt(u)

（2）回文串的长度len(u)

（3）可以不保存具体的字符串信息

为了方便，我们规定，偶回文树树根len(rt0)=0，奇回文树树根len(rt1)=−1。

转移边

转移边u→v对节点的意义是，将u对应的回文串左右两边加上同一个字符c得到节点v对应的回文串。

失配边

指向该节点对应子串的最长回文后缀

为了方便我们规定偶回文树树根rt0指向奇回文数根rt1

节点信息转移

记对应回文串出现的次数cnt(u),则 $$cnt(u)=\sum _{v=son(u)} {cnt(v)}$$

记对应回文串的长度len(u)，若节点v是由节点u转移而来的，则有len(v)=len(u)+2

构造

和后缀自动机类似，用增量法构造，每次在母串后插入一个字符，更新PAM的复杂度是O(1)的，因此构造自动机是O(n)的。

我们记录上一次插入节点的位置last，对于新插入的字符c，我们检查之前的最长回文后缀的前一个字母是否和c相同，如果相同，那么就创建一个新的节点，否则我们沿着适配边找最长回文后缀的最长回文后缀（稍微有点绕口） 如当前的母串是 $$caba$$ 现在我要插入新的字符 b。

那么我先看到最长回文后缀aba的前一个字母是c，和新插入的字符a不同（因此cabab不能组成回文子串），因此我沿着失配边找到aba的最长回文后缀a，由于前一个字符b与新插入的字符相同，能组成新回文子串aba，因此新建节点。

稍微注意的是s[0]赋值为一个特殊字符。

模板如下：

#include <bits/stdc++.h>#define rep(i, a, b) for (int i=a; i<=b; i++)#define drep(i, a, b) for (int i=a; i>=b; i--)#define inf 1e9using namespace std;typedef long long ll;const int maxn=300010;char s[maxn];int n;struct Ptree {
    int last;
    struct Node {
        int cnt, lenn, fail, son[27];
        Node(int lenn, int fail):lenn(lenn), fail(fail), cnt(0){
            memset(son, 0, sizeof(son));
        };
    };
    vector<Node> st;
    inline int newnode(int lenn, int fail=0) {
        st.emplace_back(lenn, fail);
        return st.size()-1;
    }
    inline int getfail(int x, int n) {
        while (s[n-st[x].lenn-1] != s[n]) x=st[x].fail;
        return x;
    }
    inline void extend(int c, int i) {
        int cur=getfail(last, i);
        if (!st[cur].son[c]) {
            int nw=newnode(st[cur].lenn+2, st[getfail(st[cur].fail, i)].son[c]);
            st[cur].son[c]=nw;
        }
        st[ last=st[cur].son[c] ].cnt++;
    }
    void init() {
        scanf("%s", s+1);
        n=strlen(s+1);
        s[0]=0;
        newnode(0, 1), newnode(-1);
        last=0;
        rep(i, 1, n) extend(s[i]-'a', i);
    }
    ll count() {
        drep(i, st.size()-1, 0) st[st[i].fail].cnt+=st[i].cnt;
        ll ans=0;
        rep(i, 2, st.size()-1) ans=max(ans, 1LL*st[i].lenn*st[i].cnt);
        return ans;
    }}T;int main() {
    T.init();
    printf("%lld\n", T.count());}