斯坦纳树Steiner Tree实例讲解

说到斯坦纳树问题，它是一种组合优化问题，与最小生成树相似，是最短网络的一种。最小生成树是在给定的点集和边中寻求最短网络使所有点连通。而最小斯坦纳树允许在给定点外增加额外的点，使生成的最短网络开销最小。

一、斯坦纳树

斯坦纳树问题是组合优化问题，与最小生成树相似，是最短网络的一种，其实最小生成树是最小斯坦纳树的一种特殊情况，最小生成树是在给定的点集和边中寻求最短网络使所有点连通，而最小斯坦纳树允许在给定点外增加额外的点，使生成的最短网络开销最小。

二、问题的提出

平原上的三个城镇间要兴建一个公用的煤气供应站，在选址问题上，要考虑的主要问题是使由供应站到三个城镇的输送管道的总长最短。如何去寻找合适地点？

假若要建的是一个垃圾处理站，要修建三条公路将垃圾站与三个城镇连起来。这时，因为三个城镇的居民的数目或工业性质等的不同，每天运送垃圾使用的车辆数目 各不相同，运输的费用也就各异。因此，选取地点时，如果仍考虑使三条公路的总长最小，就不合理了。

这时应该考虑：先计算出三个城镇单位时间内生产的垃圾数量的百分比（或每日运输费用的百分比），如何选取地点，使得每个城镇垃圾运输数量与公路里程的乘积之和为最小。

1638年，法国数学家费马在他所写的一本关于求极值的书中就有了第一个问题，称为费马问题

第二个问题则到了18世纪中叶才由辛普森（A.R.Simpson）提出来。

三、性质

Pollak−Gilbert猜想：

平面上任意n点集，斯坦纳最小树长与最小生成树之长的比值的最小值是

四、求解

这个问题比较现实，没有太多需要解释的地方

我们直接看解决方法：

首先我们知道，最优解必然是一棵树，这棵树又是由若干棵子树合并成的；

于是我们可以状态压缩，把 k 个节点的连通状态用一个二进制数 j 表示；

dp[i][j]表示以 i 为根，与对应状态为 j 的节点连通的子树的最小权值。

有两种转移方法：

枚举子树的形态：dp[i][j]=min(dp[i][j]，dp[i][k]+dp[i][l])，其中 k 和 l 是对j的一个划分

按照边进行松弛：dp[i][j]=min(dp[i][j]，dp[i′][j]+w[i][i′])，其中 i 和 i′ 之间有边相连

对于第一种转移，我们直接枚举子集就行了

对于第二种转移，我们仔细观察可以发现这个方程和最短路的约束条件是很类似的，于是我们可以用spfa或者dijkstra来进行状态转移

枚举子集的复杂度，spfa的复杂度为

所以总复杂度为

五、实例

给定一个包含个结点和条带权边的无向连通图。

再给定包含个结点的点集，选出的子图，使得：

1. 

2. 为连通图；

3. 中所有边的权值和最小。

你只需要求出中所有边的权值和。

输入格式

第一行：三个整数，表示的结点数、边数和的大小。

接下来行：每行三个整数，表示编号为的点之间有一条权值为的无向边。

接下来一行：个互不相同的正整数，表示的元素。

输出格式

第一行：一个整数，表示中边权和的最小值。

输入输出样例

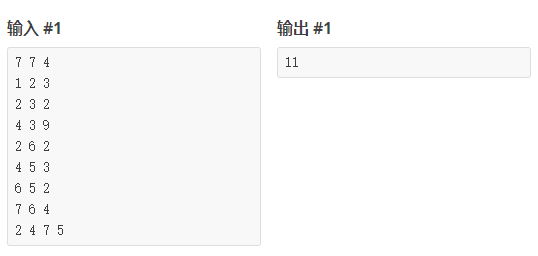
说明/提示

【样例解释】

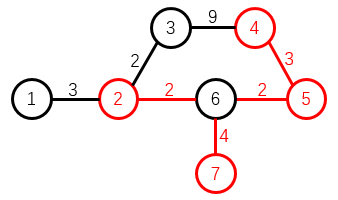
样例中给出的图如下图所示，红色点为中的元素，红色边为的元素，此时中所有边的权值和为 2+2+3+4=11，达到最小值。

【数据范围】

对于 100% 的数据，1≤≤100,  1≤≤500,  1≤≤10,  1≤,v≤,  1≤≤ 。

保证给出的无向图连通，但可能存在重边和自环。

参考代码如下：

#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#define iinf 0x3f3f3f3f
#define linf (1ll<<60)
#define eps 1e-8
#define maxn 110
#define maxk 10
#define maxe 1010
#define cl(x) memset(x,0,sizeof(x))
#define rep(i,a,b) for(i=a;i<=b;i++)
#define drep(i,a,b) for(i=a;i>=b;i--)
#define em(x) emplace(x)
#define emb(x) emplace_back(x)
#define emf(x) emplace_front(x)
#define fi first
#define se second
#define de(x) cerr<<#x<<" = "<<x<<endl
using namespace std;
using namespace __gnu_pbds;
typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
ll read(ll x=0)
{
    ll c, f(1);
    for(c=getchar();!isdigit(c);c=getchar())if(c=='-')f=-f;
    for(;isdigit(c);c=getchar())x=x*10+c-0x30;
    return f*x;
}
struct Graph
{
    int etot, head[maxn], to[maxe], next[maxe], w[maxe];
    void clear(int N)
    {
        for(int i=1;i<=N;i++)head[i]=0;
        etot=0;
    }
    void adde(int a, int b, int c=0){to[++etot]=b;w[etot]=c;next[etot]=head[a];head[a]=etot;}
    #define forp(_,__) for(auto p=__.head[_];p;p=__.next[p])
}G;
ll f[maxn][(1ll<<maxk)+10], n, m, k;
void dijkstra(ll s)
{
    priority_queue<pll,vector<pll>,greater<pll>> heap;
    ll i;
    rep(i,1,n)if(f[i][s]<linf)heap.em(pll(f[i][s],i));
    while(!heap.empty())
    {
        auto pr = heap.top(); heap.pop();
        if(pr.first!=f[pr.second][s])continue;
        forp(pr.second,G)
        {
            ll to = G.to[p];
            if(pr.first + G.w[p] < f[to][s])
            {
                f[to][s] = pr.first + G.w[p];
                heap.em( pll(f[to][s],to) );
            }
        }
    }
}
ll p[maxn];
int main()
{
    ll i, s, sub;
    n = read(), m = read(), k = read();
    rep(i,1,m)
    {
        ll u=read(), v=read(), w=read();
        G.adde(u,v,w);
        G.adde(v,u,w);
    }
    rep(i,1,n)rep(s,0,(1<<k)-1)f[i][s]=linf;
    rep(i,1,k)
    {
        p[i]=read();
        f[p[i]][1<<i-1]=0;
    }
    rep(s,0,(1<<k)-1)
    {
        rep(i,1,n)
            for(sub=s&(s-1);sub;sub=s&(sub-1))
                f[i][s] = min( f[i][s], f[i][sub] + f[i][s^sub] );
        dijkstra(s);
    }
    ll ans=linf;
    rep(i,1,n)ans=min(ans,f[i][(1<<k)-1]);
    printf("%lld",ans);
    return 0;
}