DFS求有向图(无向图)两点间路径

本文会围绕算法中DFS求有向图或无向图两点间所有路径，先讲解DFS以及有向图或无向图的意思。

有向图在图中的边是有方向的，表现出来就是有个箭头指示方向，节点只能单向通信或传递消息，相当于单行道，无向图边没方向是双向的，边连接的两个节点有通路可以双向通信，类似于双行道。

无向图，边没有方向的图称为无向图。邻接矩阵则是对称的，且只有0和1，因为没有方向的区别后，要么有边，要么没边。

DFS作为搜索算法，最常用于图，对图的遍历，探寻路径，甚至是求一些情况下的最短路。我在这里就介绍一下dfs求两点的的所有路径。

以这张图为介绍，v1是出发点，v3是终点。

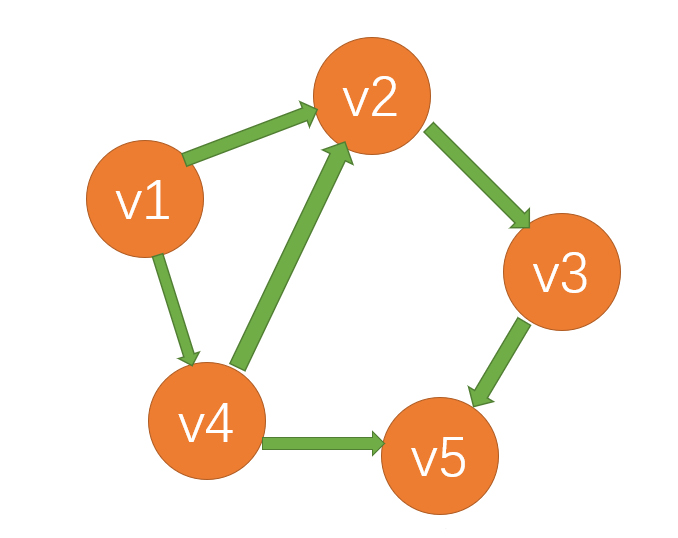
（1）v1开始出发，v1被标记访问过，并入栈，到v2，标记并入栈；

（2）到v3，此时v3是终点，到达函数开始的判断条件，输入堆栈经过的路径。一条路找到（1,2,3）。此时虽然v3可以到v5，但也没有必要探寻下去：算法的角度来说如果继续探寻下去v3就会被标记，就算有路可以到，下次就不会背进入递归了；实际应用来说也没必要绕一圈再到一个地方。这算是一个剪枝吧。

（3）v3回溯到v2，v2没有可走的路了，堆栈中的v2出栈，v2并取消标记；

（4）v2回溯到v1，有v4可走，入栈并标记。探寻v2可走，入栈并标记。v2到v3，另一条路找到（1,4,2,3）；

（5）从v3回溯到v4，探寻到v5可走，入栈并标记；

（6）v5没路可走了，回溯到v4到v1，程序结束。

算法时间复杂度是O(n*m)。

输入样例

5 6

1 2
2 3
3 5
1 4
4 2
4 5

1 3

输出样例

1 2 3
1 4 2 3

代码如下：

#include<stdio.h>
#include<math.h>
int map[100][100]={0};///map[i][j]为0表示i, j两点之间不通，为1表示有一条路
int stack[120],v[100]={0},top=0,m,n,start,end;
void dfs(int pos)//从pos点开始访问
{
	int i;
	if(pos==end){//到达终点
		for(i=0;i<top;i++)
			printf("%d ",stack[i]);
		printf("%d\n",end);	
		return;
	}
	v[pos]=1;//标记被访问过 
	stack[top++]=pos;//经过的路径加入队列
	for(i=1;i<=n;i++){
		if(!v[i]&&map[pos][i])//如果这个点没有被访问过，而且b与这个点相连，就继续搜索
			dfs(i);
	}
	v[pos]=0;//删除标记 
	top--;//队列里删除b
}

int main()
{
    int i,x,y;
    printf("分别输入顶点数n和路径数m："); 
    scanf("%d %d",&n,&m);//n是顶点数，m是边数 
    
    printf("输入m条路径："); 
    for(i=1; i<=m; i++) {
        scanf("%d %d", &x,&y);
        map[x][y] = 1;//这两点之间有路径
		//map[y][x] = 1; //无向图加上这一句即可 
    }
    
    printf("输入起始点和终点：");
    scanf("%d %d", &start,&end);
    
    printf("\n程序执行结果为：\n"); 
    dfs(start);
    return 0;
    
}

知道每条路径的长度也很容易，输入信息的时候加上路径长度，函数多一个参数，每次递归的时候加上这两点路径的长度，到达终点输出就行了，求最短路的话每次到终点比较一下即可。