说到数位DP，它主要是用于处理一些与数位有关的问题，主要是计数问题。并且数位DP一直以来是DP家族里比较冷门的一种，但一旦遇上了，如果不会数位DP单纯靠暴力方法很难骗分。
一、什么是数位DP？
数位DP是一种计数用的DP，一般就是要统计一个区间[l,r]内满足一些条件数的个数。所谓数位DP，字面意思就是在数位上进行DP。数位还算是比较好听的名字，数位的含义：一个数有个位、十位、百位、千位......数的每一位就是数位！
之所以要引入数位的概念完全就是为了DP。数位DP的实质就是换一种暴力枚举的方式，使得新的枚举方式满足DP的性质，然后记忆化就可以了。
数位DP往往都是这样的题型，给定一个闭区间[l,r]，让你求这个区间中满足某种条件的数的总数。而这个区间可能很大，简单的暴力代码如下：
int ans=0;
for(int i=l;i<=r;i++){
if(check(i))ans++;
}我们发现，若区间长度超过1e8，我们暴力枚举就会超时了，而数位DP则可以解决这样的题型。数位DP实际上就是在数位上进行DP。
数位DP解法
数位DP就是换一种暴力枚举的方式，使得新的枚举方式符合DP的性质，然后预处理好即可。
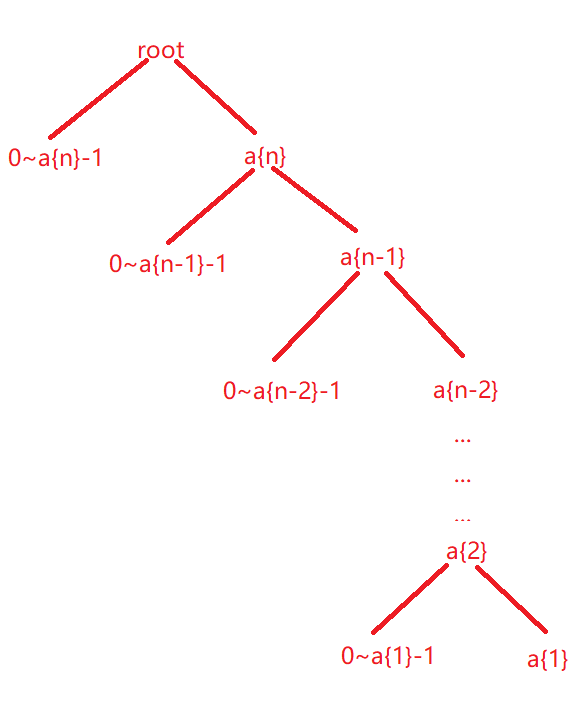
我们来看：我们可以用f(n)表示[0,n]的所有满足条件的个数，那么对于[l,r]我们就可以用[l,r]⟺f(r)−f(l−1)，相当于前缀和思想。那么也就是说我们只要求出f(n)即可。那么数位DP关键的思想就是从树的角度来考虑。将数拆分成位，从高位到低位开始枚举。我们可以视N为n位数，那么我们拆分
。那么我们就可以开始分解建树，如下。之后我们就可以预处理再求解f(n)了，个人认为求解f(n)是最难的一步。
听完是不是有点绕，我们可以来点题目练习一下，做完就会发现了数位DP的套路了。
二、数位DP经典例题
例题：度的数量
题目：求给定区间 [X,Y] 中满足下列条件的整数个数：这个数恰好等于K个互不相等的B的整数次幂之和。例如，设 X=15,Y=20,K=2,B=2，则有且仅有下列三个数满足题意：
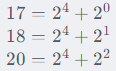
输入格式
第一行包含两个整数 X 和 Y，接下来两行包含整数 K 和 B 。
输出格式
只包含一个整数，表示满足条件的数的个数。
数据范围
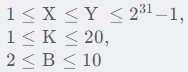
输入样例：
15 20
2
2
输出样例：
3
解题思路
此题实际上就是将十进制数转化为B进制数，判断位数上的值是否为1。那么我们可以视N为n位数，那么我们拆分
。从树的角度考虑：我们设N=76543210，B=10，那么我们从高位往最低位开始枚举如下；枚举
时，我们有两种选择：
（1）走右边分支，那么我们填
，而题目要求每一位只能填1或者0,而
，所以不是合法方案，我们直接剔除。
（2）走左边分支，那么我们可以填0~6，即
，那么由于每一位只能填1或者0，所以我们累加这两种选择的方案。
记住，走到了左边分支是可以直接累加的。
所以我们实际上还是要做一个预处理的，我们用f[i][j]表示还剩下i位没有填，且需要填写j个1的方案数。那么在(i,j)这个状态，我们可以选择填1，那么接下来的状态就是f[i−1][j−1]，而如果填0，那么接下来的状态就是f[i−1][j]，那么状态转移方程就是f[i][j]=f[i-1][j]+f[i][j−1]。而初始状态即是当j=0时，f[i][0]=1。这样我们就可以预处理f数组了。
处理完之后我们就可以直接模拟做了。
代码如下：
/**
*@filename:度的数量
*@author: pursuit
*@csdn:unique_pursuit
*@email: 2825841950@qq.com
*@created: 2021-05-12 11:23
**/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 100000 + 5;
const int mod = 1e9+7;
int l,r,k,b;
int f[35][35];
//首先我们先预处理f数组。其中f[i][j]表示剩下还有i个没填，需要填写j个1的方案数。
void init(){
for(int i=0;i<35;i++){
for(int j=0;j<=i;j++){
if(!j)f[i][j]=1;
else{
f[i][j]=f[i-1][j]+f[i-1][j-1];
}
}
}
}
int dp(int n){
//求解f(n)。我们需要避免n为0的情况，这里需要特判。
if(!n)return 0;
vector<int> nums;//将n分割，存储位数。
while(n){
nums.push_back(n%b);
n/=b;
}
int ans=0;//答案。
int last=0;//前面的信息，这里代表的是前面分支选取了多少个1.
for(int i=nums.size()-1;i>=0;i--){
int x=nums[i];
if(x){
//说明x>0，我们可以选择左边分支填0.
ans+=f[i][k-last];
if(x>1){
//当x>1我们才可以枚举左边分支填1.
if(k-last-1>=0){
//如果还可以填1的话。
ans+=f[i][k-last-1];
}
break;//因为右边分支只能为0或1，所以不符合条件。break。
}
else{
//当x=1就可以进入右边的分支继续讨论。
last++;
if(last>k)break;
}
}
//考虑到最后一位，如果符合条件那么末位填0也算一种方案。
if(!i&&last==k)ans++;
}
return ans;
}
void solve(){
}
int main(){
cin>>l>>r>>k>>b;
init();
cout<<dp(r)-dp(l-1)<<endl;
solve();
return 0;
}C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程，并配有习题和答疑，点击了解：
一点编程也不会写的：零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码？手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程：算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程