矩阵树定理也称Matrix-Tree定理或Kirchhoff定理。这个定理提供了一种方式使用一个特殊的矩阵的行列式来计算一个图的生成树的数量。
对于一个无向图来说,我们可以构造它的Laplace矩阵L,其中:
如果节点i有度为d,那么L[i,i] = d
如果节点i和节点j之间有边相连,那么L[i,j] = L[j,i] =-1
其他情况L[i,j]=0
例如下图的Laplace矩阵:
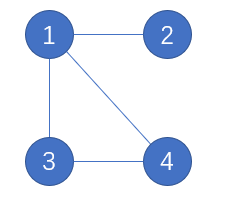
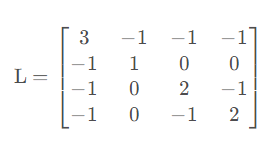
那么我们从L中任意删除某一行和某一列剩下的矩阵,对其求行列式,例如删除第一行和第一列:
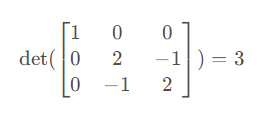
那么这个图的生成树的数量为3,可以证明删除任意行列的行列式的值不变。
注意,Cayley定理是矩阵树定理的一个特殊情况,因为Cayley定理说明,一个n个节点的组成树的数量为![]() 这正好是n个节点完全图的生成树的数量,因为:
这正好是n个节点完全图的生成树的数量,因为:

去掉第一行第一列之后:
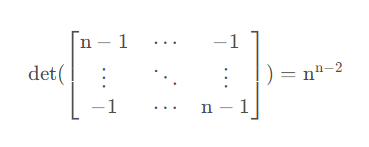
例题:
你突然有了一个大房子,房子里面有一些房间。事实上,你的房子可以看做是一个包含n×m个格子的格状矩形,每个格子是一个房间或者是一个柱子。在一开始的时候,相邻的格子之间都有墙隔着。
你想要打通一些相邻房间的墙,使得所有房间能够互相到达。在此过程中,你不能把房子给打穿,或者打通柱子(以及柱子旁边的墙)。同时,你不希望在房子中有小偷的时候会很难抓,所以你希望任意两个房间之间都只有一条通路。现在,你希望统计一共有多少种可行的方案,答案对![]() 取模。
取模。
输入格式:
第一行两个整数n,m。
接下来n行,每行m个字符 . 或 *,其中 . 代表房间,* 代表柱子。
输出格式:
一行一个整数,表示合法的方案数对![]() 取模后的值。
取模后的值。
输入输出样例
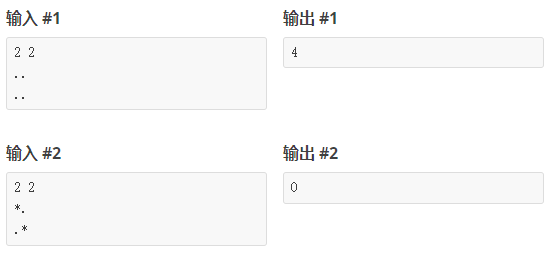
说明/提示
数据规模与约定
对于20%的数据,n,m≤3。
对于50%的数据,n,m≤5。
有40%的数据,min(n,m)≤3。
有30%的数据,不存在柱子。
对于100%的数据,1≤n,m≤9
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 | #include <bits/stdc++.h>using namespace std;#define FR freopen("in.txt", "r", stdin)#define FW freopen("out.txt", "w", stdout)typedef long long ll;int mp[15][15];ll laplace[100][100];int n, m;int pos[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};int tot = 1;const ll mod = 1000000000;int main(){ scanf("%d %d", &n, &m); for (int r = 1; r <= n; r++) { for (int c = 1; c <= m; c++) { char t; scanf(" %c", &t); if (t == '.') { mp[r][c] = tot++; } } } for (int r = 1; r <= n; r++) { for (int c = 1; c <= m; c++) { if (mp[r][c] == 0) continue; for (int p = 0; p < 4; p++) { int dr = r + pos[p][0]; int dc = c + pos[p][1]; if (mp[dr][dc] == 0) continue; laplace[mp[r][c]][mp[r][c]]++; laplace[mp[r][c]][mp[dr][dc]] = laplace[mp[dr][dc]][mp[r][c]] = -1; } } } // 化上三角矩阵 tot--; ll sgn = 1; for (int r = 1; r < tot; r++) { int d = r; for (int k = r; k < tot; k++) { if (laplace[k][r] != 0) { d = k; break; } } swap(laplace[d], laplace[r]); if (laplace[r][r] == 0) { printf("0"); return 0; } for (int k = r + 1; k < tot; k++) { while (laplace[k][r] != 0) { swap(laplace[r], laplace[k]); sgn *= -1; ll di = laplace[k][r] / laplace[r][r]; for (int j = r; j < tot; j++) { laplace[k][j] = ((laplace[k][j] - laplace[r][j] * di) % mod + mod) % mod; } } } } ll ans = 1; for (int i = 1; i < tot; i++) { ans = ((ans * laplace[i][i]) % mod + mod) % mod; } ans = (ans * sgn + mod) % mod; printf("%lld", ans); return 0;} |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程