什么是 “并查集” ?
并查集,是一种可以使用代表元来表示不相交集的数据结构,在一些只需要查询两个元素是否属于同一个集合的情况下它很有用。比如给定一个无向图,判断两个顶点是否属于同一个连通分量。
在很多算法里面都会用到它,比如Kruskal最小生成树算法。
并查集被很多OIer认为是最简洁而优雅的数据结构之一,主要用于解决一些元素分组的问题。它管理一系列不相交的集合,并支持两种操作:
合并(Union):把两个不相交的集合合并为一个集合。
查询(Find):查询两个元素是否在同一个集合中。
当然,这样的定义未免太过学术化,看完后恐怕不太能理解它具体有什么用。所以我们先来看看并查集最直接的一个应用场景:亲戚问题。
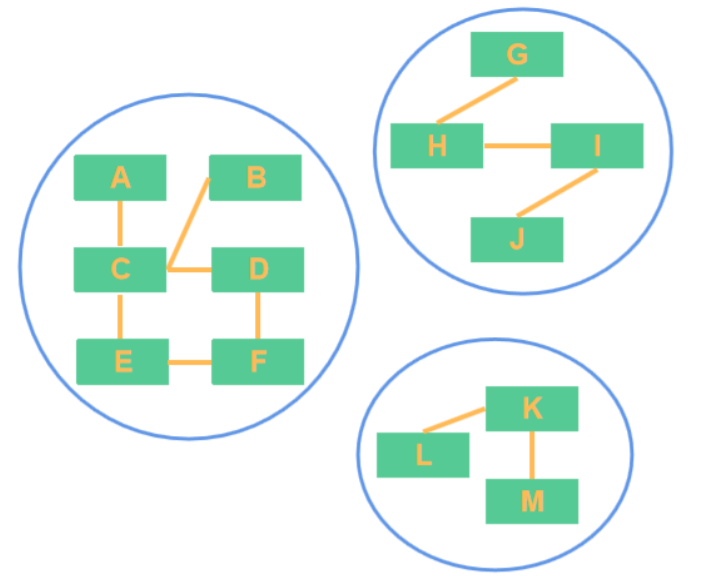
并查集的操作
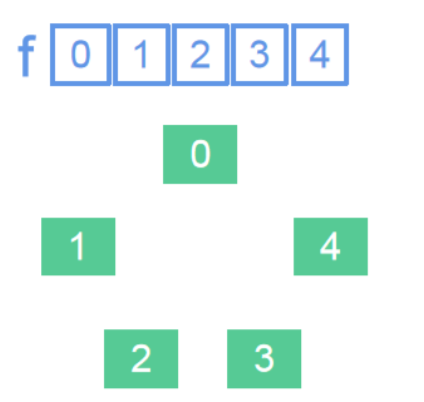
1. 初始化
并查集的思想是通过标记确定该顶点所在的组。
所以对于一个n个点,m条边的图,我们需要新建一个长度为n的数组f(可以理解为father),f[n]代表点n的团伙“代表人”,当两个点所在团伙“代表人”相同,则这两个点所在团伙相同。
而在最开始,每个顶点间都是互相不连通的,所以每个顶点单独属于一个团伙,每个顶点理所应当成为自己团伙的“代表人”,所以我们把f[n]的初始值赋为n。
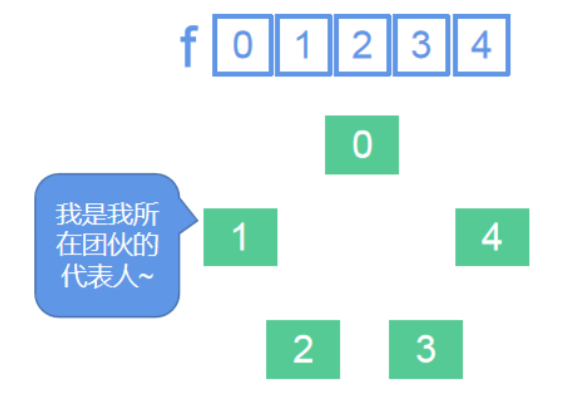
2. 合并团伙
我们以连接3和1这两个点做例子:
在连接点3和点1时,3和1形成了一个团伙,而3和1的团伙代表人f[3]和f[1]就应该统一,具体是让3做代表人还是让1做代表人随便,我们让1做代表人。f[3] = 1,这条语句可以理解为让1所在团伙的代表人同时成为3所在团伙的代表人。
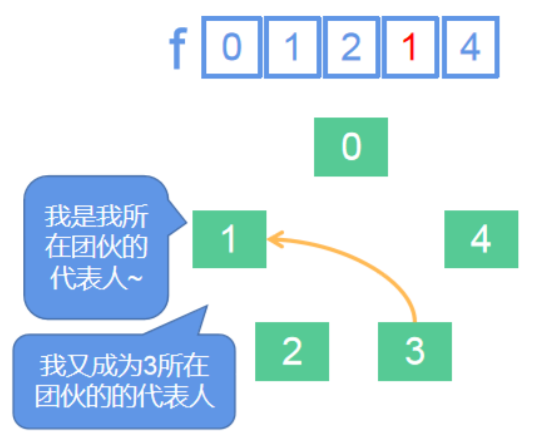
(箭头只是体现了f数组中“团伙成员”和“代表人”的关系,其实这个图是无向图)
可是,像f[a] = b这样合并真的对吗?请大家考虑这样一种情况。
刚刚我们合并了3和1,现在我们需要合并3和2。如果按照f[a] = b这样合并,那么,f[3]就被赋值为了2。这样,f[3]原本的值1就被覆盖了,也就是说,1和3的团伙就被硬生生地“拆散”了。
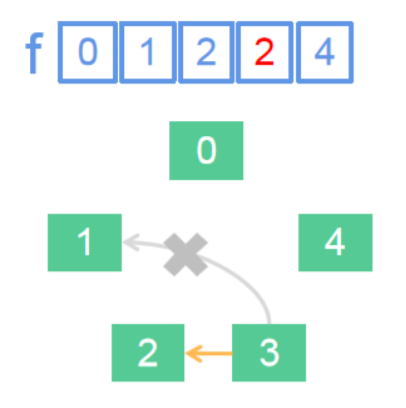
下面我们换一个例子:合并3和4。此时我们不应该令f[3] =4,应该让f[3的团伙代表人] = (4的团伙代表人),如下图。
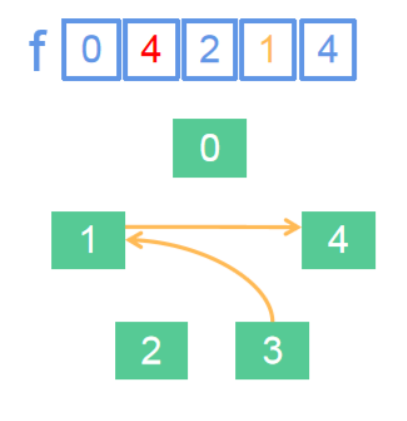
这样,合并两个团伙的工作就完成了。总结起来就一句话:f[a的团伙代表人] = (b的团伙代表人)。
3. 查找团伙代表人
紧接着,又一个问题浮出水面:根据上面的公式f[a的团伙代表人] = (b的团伙代表人),可是a、b的团伙代表人怎么求?是f[a]吗?不不不,这里的情况变得复杂了。大家再次考虑一种特殊情况。
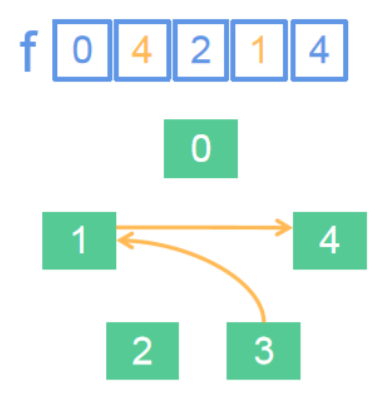
在这种情况下,3的团伙代表人是谁?1还是4?正确答案是4。因为,一个团伙中每一个点都直接或间接地“指向”这个团伙的代表人。(1,3,4)这个团伙中,1直接地指向4,3间接地指向4,所以4才是这个团伙里的代表人。
那么,点x的团伙代表人怎么求呢?我们会发现另一个特征,任何一个团伙的代表人a,都有f[a] = a。很好理解,团伙代表人也是团伙的一个成员,团伙代表人所在团伙的代表人就是它自己。
而对于其他点a,f[a]均不等于a。并且如果一个顶点a有f[a] ≠ a,那么这个点一定不是团伙的代表人,因为f[a]不会间接地或直接地指向a(并查集保证不会存在环)。
根据这一特性,我们可以判断点a是否为某个团伙的代表人。
在例子中,我们想要知道1是否为团伙代表人,就可以看f[1]是否等于1,很明显,f[1] = 4,所以1不是该团伙的代表人,我们要继续“追本溯源”,对5进行判断。这个过程就是一种递归的寻找过程。
知道了这个特性,我们就可以写出相应的C++代码(这里还给出了循环版的代码,根据情况使用):
1 2 3 | int getFather(int x) { return f[x] == x ? x : getFather(f[x]);} |
1 2 3 4 5 | int getFather(int x) { while (f[x] != x) x = f[x]; return x;} |
这是一个递归函数,如果f[x] = x,说明这个点已经是该团伙的代表人,直接返回就好了,如果它不是该团伙的代表人,那么就返回自己指向的点的团伙代表人。
在求getFather(3)时,f[3] != 3,返回getFather(f[3])也就是getFather(1);
在求getFather(1)时,f[1] != 1,返回getFather(f[1])也就是getFather(4);
在求getFather(4)时,f[4] == 4,返回4。递归结束。最后计算出3的团伙代表人是4。
4. 查询顶点是否在同一团伙
并查集的最后一种操作叫做查询,就是查询两个点是否连通(在同一团伙)。
前面已经介绍过,当两个点所在团伙“代表人”相同,则这两个点所在团伙相同。判断两个点a、b在同一团伙的方法就是:
1 | getFather(a) == getFather(b) |
5. 完整代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | const int N = 100; // 节点数量int f[N];int init() { // 初始化 for (int i=0; i<N; i++) f[i] = i;}int getFather(int x) { // 查询所在团伙代表人 return f[x]==x ? x : getFather(f[x]);}int merge(int a, int b) { // 合并操作 f[getFather(a)] = getFather(b);}bool query(int a, int b) { // 查询操作 return getFather(a) == getFather(b);}int main() { init(); merge(3, 1); // 3和1是亲戚 merge(1, 4); // 1和4是亲戚 cout << getFather(3) << endl; // 输出3的团伙代表人+换行 cout << query(3, 1) << endl; // 输出3和1是否是亲戚+换行} |
是不是觉得并查集非常的巧妙!我们既没有构建图,也没有构建边,自始至终只用到了f数组,又优化了时间。
不要小瞧并查集代码短,在很多时候并查集都会派上用场,比如著名的克鲁斯卡尔算法,就是通过并查集判断两个顶点是否相连的。更重要的是体会并查集的思想,用这种思想来优化代码。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程