本篇将会结合实例解析宽度优先搜索(BFS)。
一、BFS概念
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
所谓广度,就是一层一层的,向下遍历,层层堵截,还是这幅图,我们如果要是广度优先遍历的话,我们的结果是V1 V2 V3 V4 V5 V6 V7 V8。
(1)访问顶点vi ;
(2)访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
(3)依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的顶点的邻接点都被访问;
二、BFS(广度优先搜索)
广度优先搜索较之深度优先搜索之不同在于,深度优先搜索旨在不管有多少条岔路,先一条路走到底,不成功就返回上一个路口然后就选择下一条岔路,而广度优先搜索旨在面临一个路口时,把所有的岔路口都记下来,然后选择其中一个进入,然后将它的分路情况记录下来,然后再返回来进入另外一个岔路,并重复这样的操作,用图形来表示则是这样的。
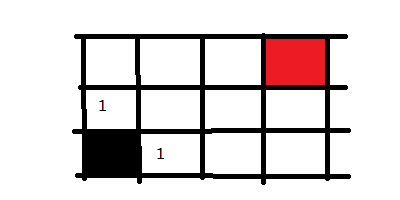
从黑色起点出发,记录所有的岔路口,并标记为走一步可以到达的。然后选择其中一个方向走进去,我们走黑点方块上面的那个,然后将这个路口可走的方向记录下来并标记为2,意味走两步可以到达的地方。
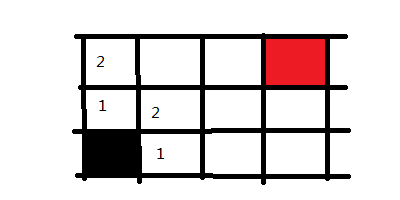
接下来,我们回到黑色方块右手边的1方块上,并将它能走的方向也记录下来,同样标记为2,因为也是走两步便可到达的地方。
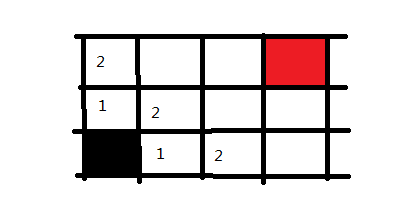
这样走一步以及走两步可以到达的地方都搜索完毕了,下面同理,我们可以迅速把三步的格子给标记出来。
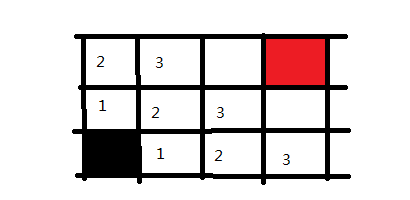
再之后是四步,五步。
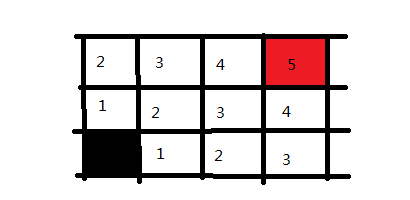
我们便成功寻找到了路径,并且把所有可行的路径都求出来了。在广度优先搜索中,可以看出是逐步求解的,反复的进入与退出,将当前的所有可行解都记录下来,然后逐个去查看。在DFS中我们说关键点是递归以及回溯,在BFS中,关键点则是状态的选取和标记。
三、例题
(1)题目一:
一位农夫在点n上,他要到奶牛所在的点k上,他可以每次从点X到点X-1或点X+1或点2*X,问他到达点k的最短次数.(0 ≤ N ≤ 100,000,0 ≤ K ≤ 100,000)
样例:
Sample Input
5 17
Sample Output
4
思路:看到这一道题,第一反应就是看看能否找到规律,然而很显然它没有规律可言,我们需要靠一种近似暴力的方法,而DFS在这里是行不通的,于是只能用BFS来解这道题了。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | #include <iostream>#include <stdio.h>#include <cstring>#include<queue>#define pp pair<int,int>using namespace std;int n,k,ans;queue<pp>q;bool v[200004];void bfs() { q.push(pp(n,0));//先将n丢进队列 v[n]=1; while(!q.empty()) { if(q.empty())break; pp now=q.front(); q.pop(); if(now.first==k) { ans=now.second; break; } now.second++;//接下来我们有3种操作,将现在的位置now.second 加1 或 减1 或 乘2 if(!v[now.first+1]&&now.first<k) {//边界条件不能少了 q.push(pp(now.first+1,now.second)); v[now.first+1]=1;//将已经走过的点标记为1,为什么呢??q队列中到这个数的次数是从小到大排序的,now.first+1这个点刚通过now.first被拜访过,它的此时次数肯定小于等于下一次拜访的次数.想一想为什么. } if(!v[now.first-1]&&now.first-1>=0) { q.push(pp(now.first-1,now.second)); v[now.first-1]=1; } if(now.first<k&&(!v[now.first*2])) { q.push(pp(now.first*2,now.second)); v[now.first*2]=1; } } return;}int main() { scanf("%d%d",&n,&k); bfs(); printf("%d\n",ans); return 0;} |
(2)题目二:
给你两个四位数的质数a,b,让你通过一个操作使a变成b.这个操作可以使你当前的数x改变一位上的数使其变成另一个质数,问操作的最小次数(如果没有这种方式,输出Impossible)
注意:没有前导0!!!;
例如:1033到8179可以从1033->1733->3733->3739->3779->8779->8179
样例:
Sample Input
3
1033 8179
1373 8017
1033 1033
Sample Output
6
7
0
思路:可以先将10000以内所有的质数记录下来,再进行BFS。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 | #include<iostream>#include<stdio.h>#include<cstring>#include<queue>#include<time.h>#define N 10003#define pp pair<int,int>using namespace std;int T,n,m,ans;bool v[N],vis[N],t[N];queue<pp>q;void pre() {//记录10000以内的质数 for(int i=2; i<=9999; i++) { if(!v[i]) { t[i]=1;//t[i]=1表示i是质数 for(int j=i; j<=9999; j+=i) { v[j]=1; } } }}void BFS() { q.push(pp(n,0));//先将给我们的初始数加入q队列 while(!q.empty()) { while(!q.empty()&&vis[q.front().first])q.pop(); if(q.empty())break; pp now=q.front(); vis[q.front().first]=1; q.pop(); if(now.first==m) { ans=now.second; break; } for(int i=1; i<=1000; i*=10) {//枚举位数 int r=now.first-((now.first/i)%10)*i; for(int j=0; j<=9; j++) {//枚举当前位数更改的值 if(i==1000&&j==0)continue;//特判前导0的情况!!! if(t[r+j*i]&&!vis[r+j*i]) { q.push(pp(r+j*i,now.second+1));//BFS的核心转移代码 } } } } return;}int main() { pre(); scanf("%d",&T); while(T--) { while(!q.empty())q.pop(); memset(vis,0,sizeof vis); ans=-1; scanf("%d%d",&n,&m); BFS(); if(ans==-1)printf("Impossible\n"); else printf("%d\n",ans); } return 0;} |
| 1703 | 数据结构-图的遍历-BFS广度优先搜索(广搜) |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程