本篇主要图文讲解最小生成树的实现和算法。
一、最小生成树
最小生成树(minimum spanning tree)是由n个顶点,n-1条边,将一个连通图连接起来,且使权值最小的结构。最小生成树可以用Prim(普里姆)算法或kruskal(克鲁斯卡尔)算法求出。
此外还可以用bfs和dfs生成,分别叫bfs生成树和dfs生成树。
例:
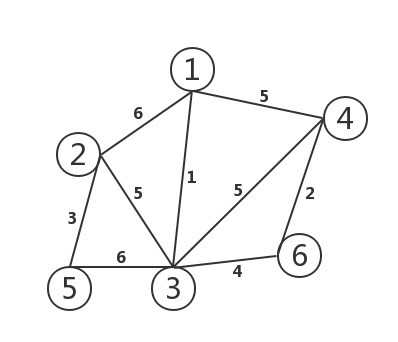
二、Prim(普里姆)算法
这里就采用的是邻接矩阵存储的,Prim和最短路中的dijkstra很像,方法:
(1)先建立一个只有一个结点的树,这个结点可以是原图中任意的一个结点。
(2)使用一条边扩展这个树,要求这条边一个顶点在树中另一 个顶点不在树中,并且这条边的权值要求最小。
(3)重复步骤(2)直到所有顶点都在树中。
如图:
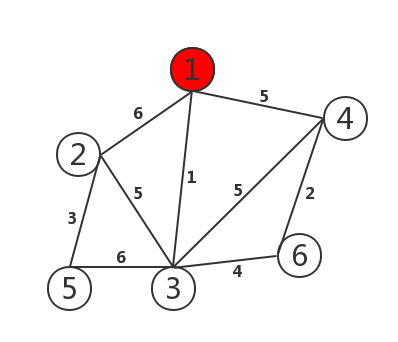
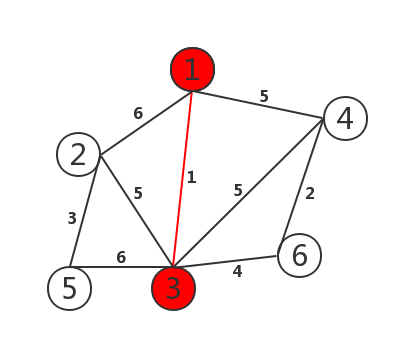
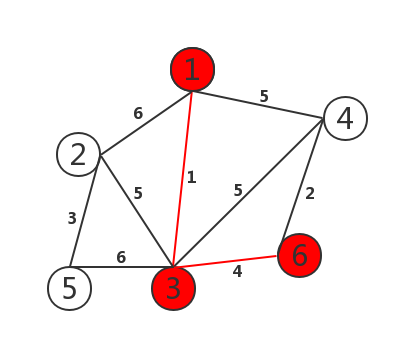
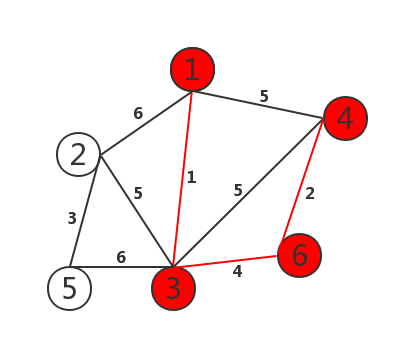
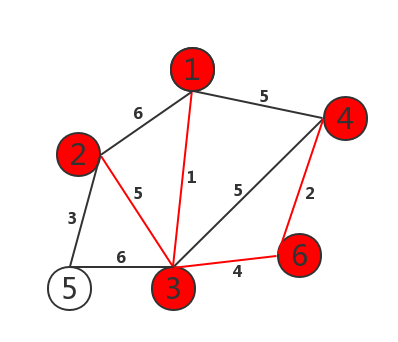
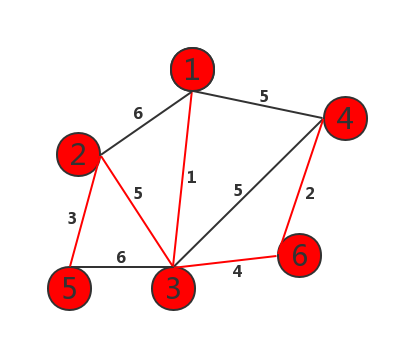
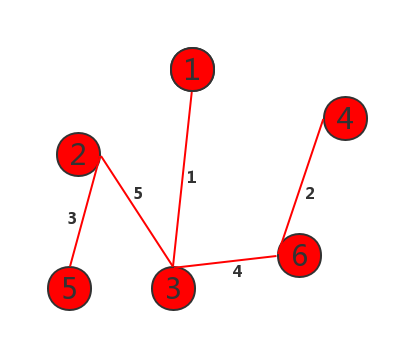
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 | #include<stdio.h>#define MAX 100#define MAXCOST 100000int graph[MAX][MAX];void prim(int graph[][MAX], int n){ int lowcost[MAX];//lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0表示i点加入了MST int mst[MAX];//表示对应lowcost[i]的起点,当mst[i]=0表示起点i加入MST int i, j, min, minid, sum = 0; for (i = 2; i <= n; i++) { lowcost[i] = graph[1][i];//lowcost存放顶点1可达点的路径长度 mst[i] = 1;//初始化以1位起始点 } mst[1] = 0; for (i = 2; i <= n; i++) { min = MAXCOST; minid = 0; for (j = 2; j <= n; j++) { if (lowcost[j] < min && lowcost[j] != 0) { min = lowcost[j];//找出权值最短的路径长度 minid = j; //找出最小的ID } } printf("V%d-V%d=%d\n",mst[minid],minid,min); sum += min;//求和 lowcost[minid] = 0;//该处最短路径置为0 for (j = 2; j <= n; j++) { if (graph[minid][j] < lowcost[j])//对这一点直达的顶点进行路径更新 { lowcost[j] = graph[minid][j]; mst[j] = minid; } } } printf("最小权值之和=%d\n",sum);}int main(){ int i, j, k, m, n; int x, y, cost; scanf("%d%d",&m,&n);//m=顶点的个数,n=边的个数 for (i = 1; i <= m; i++)//初始化图 { for (j = 1; j <= m; j++) { graph[i][j] = MAXCOST; } } for (k = 1; k <= n; k++) { scanf("%d%d%d",&i,&j,&cost); graph[i][j] = cost; graph[j][i] = cost; } prim(graph, m); return 0;} |
三、kruskal(克鲁斯卡尔)算法
Kruskal 算法是能够在O(mlogm) 的时间内得到一个最小生成树的算 法。它主要是基于贪心的思想:
(1)将边按照边权从小到大排序,并建立一个没有边的图T。
(2)选出一条没有被选过的边权最小的边。
(3)如果这条边两个顶点在T 中所在的连通块不相同,那么将 它加入图T, 相同就跳过。
(4)重复(2)和(3)直到图T连通为止。
其实这里只需要维护连通性,可以不需要真正建立图T,还可以用并查集来维护。
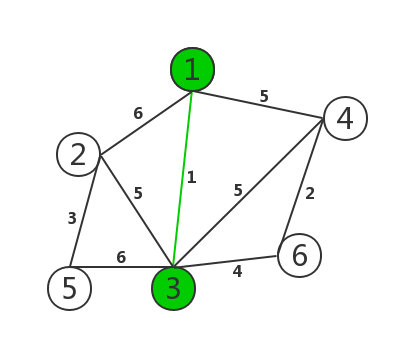
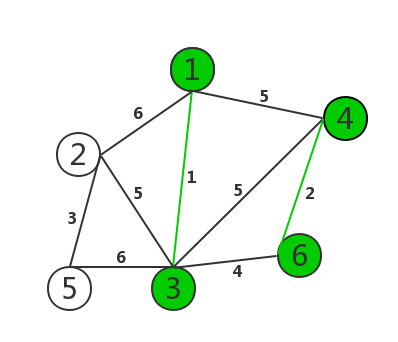
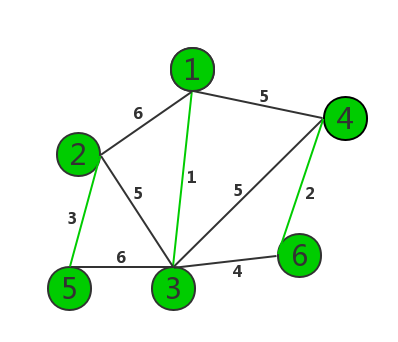
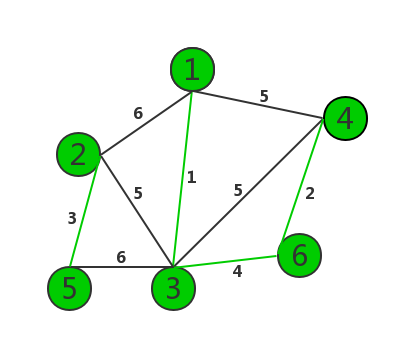
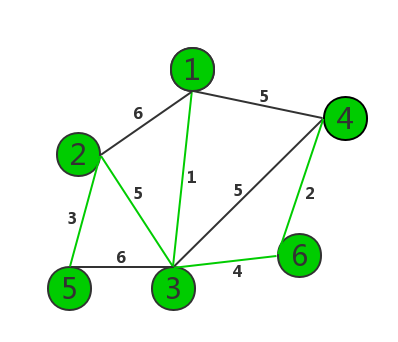
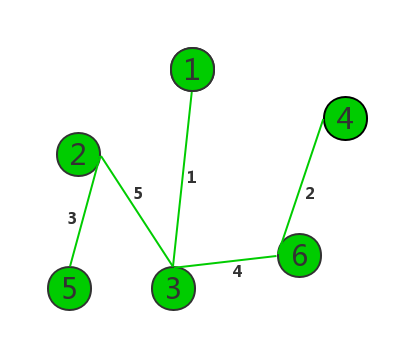
这里用邻接表(不是链表)进行操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 | #include <stdio.h>#define MAXE 100#define MAXV 100typedef struct{ int vex1; //边的起始顶点 int vex2; //边的终止顶点 int weight; //边的权值}Edge;void kruskal(Edge E[],int n,int e){ int i,j,m1,m2,sn1,sn2,k,sum=0; int vset[n+1]; //借用一个辅助数组vset[i]用来判断某边是否加入了最小生成树集合 //就是把每个顶点都看成一个连通分量,并查集数组初始化 for(i=1;i<=n;i++) //初始化辅助数组 vset[i]=i; k=1;//表示当前构造最小生成树的第k条边,初值为1 j=0;//E中边的下标,初值为0 while(k<e)//生成的边数小于e时继续循环 { m1=E[j].vex1; m2=E[j].vex2;//取一条边的两个邻接点 sn1=vset[m1]; sn2=vset[m2]; //分别得到两个顶点所属的集合编号 if(sn1!=sn2)//两顶点分属于不同的集合,该边是最小生成树的一条边 {//防止出现闭合回路 printf("V%d-V%d=%d\n",m1,m2,E[j].weight); sum+=E[j].weight; k++; //生成边数增加 if(k>=n) break; for(i=1;i<=n;i++) //两个集合统一编号 if (vset[i]==sn2) //集合编号为sn2的改为sn1 vset[i]=sn1; } j++; //扫描下一条边 } printf("最小权值之和=%d\n",sum);}//以下为快排int fun(Edge arr[],int low,int high) { int key; Edge lowx; lowx=arr[low]; key=arr[low].weight; while(low<high) { while(low<high && arr[high].weight>=key) high--; if(low<high) arr[low++]=arr[high]; while(low<high && arr[low].weight<=key) low++; if(low<high) arr[high--]=arr[low]; } arr[low]=lowx; return low; }void quick_sort(Edge arr[],int start,int end){ int pos; if(start<end) { pos=fun(arr,start,end); quick_sort(arr,start,pos-1); quick_sort(arr,pos+1,end); }}int main(){ Edge E[MAXE]; int nume,numn; //freopen("1.txt","r",stdin);//文件输入 printf("输入顶数和边数:\n"); scanf("%d%d",&numn,&nume); for(int i=0;i<nume;i++) scanf("%d%d%d",&E[i].vex1,&E[i].vex2,&E[i].weight); quick_sort(E,0,nume-1); kruskal(E,numn,nume);} |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程