上下界网络流总结

上下界网络流可以看做普通网络流的升级版，现在对于流量网络，我们不再只关注其流量的上界，而是同时关注流量的上下界。

一、无源汇有上下界可行流

这是上下界网络流中最简单的一种，给定一个没有源点和汇点、每条边的流量有上下界的流量网络，问是否存在一种可行流使得流量平衡。

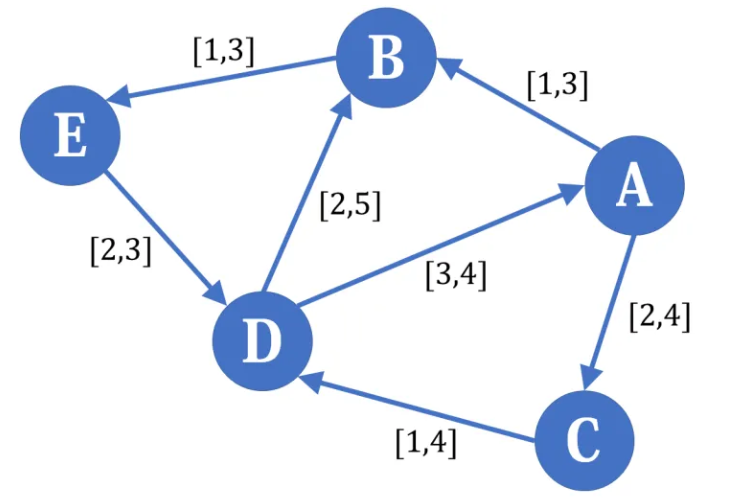
做法是，我们把它拆成两个结构与原图相同的普通网络，一个每条边的容量为原网络对应边的流量下界，另一个为对应边的流量上界与下界之差。

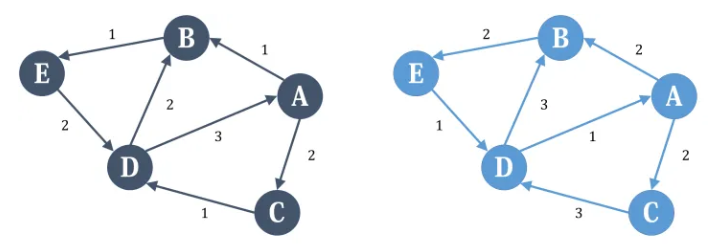
我们希望下界网络和差网络的流相加后恰好是原图的一个可行流，这首先要求下界网络是满流的（可行流必须达到每条边的下界）。但是下界网络满流后不一定流量平衡，所以我们要对差网络进行一定的修改以弥补这种不平衡。

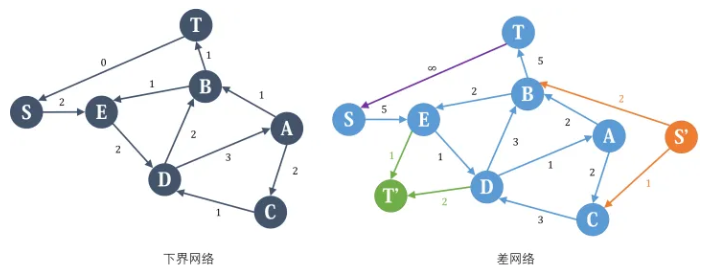
我们分别考虑下界网络的每个点。A点，流入量为3，流出量也为3，所以是平衡的，那么在差网络中，也应该是平衡的，所以不做修改。B点，流入量为3，流出量为1，流入比流出多2，所以我们希望在差网络中，B的流出应该比流入多2，于是我们在差网络中新设一个源点，然后加入一条容量为2的附加边从源点连向B，这样在差网络平衡时，除去附加边，B点的流出恰好比流入多2，C点与B点类似。D点则相反，因为我们希望在差网络中D点流入比流出多2，所以我们新设一个汇点，然后从D点连一条容量为2的附加边到汇点，E点又和D类似。

也就是说，如果下界网络中某个点有x的净流入，在差网络中我们就从源点向它连一条容量为x的附加边；相反，如果下界网络中某个点有x的净流出，在差网络中我们就从它向汇点连一条容量为x的附加边。这样，我们把差网络修改如下：

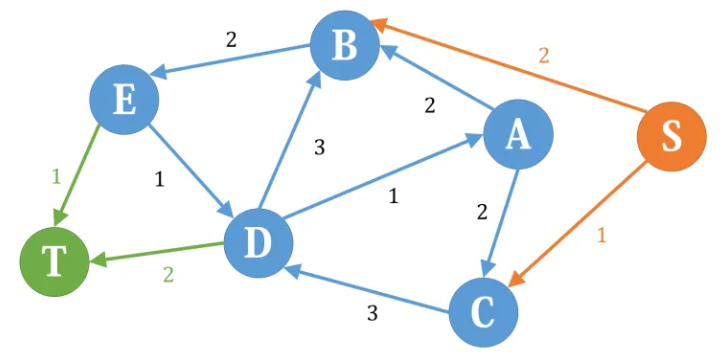
在差网络上跑一遍最大流，把每条非附加边的流，加上下界网络的满流，就是一个可行流。但是，如果跑完最大流发现，存在附加边未满流，那说明平衡条件没有得到满足，于是原图不存在可行流。

在实际中，是不需要建立下界网络的，只需要对差网络进行操作即可。另外最后判断的时候并无必要遍历所有附加边，而只需要判断所有从源点出发的边，或者判断所有连向汇点的边即可，因为根据网络流的性质，两者容量和应该相等，于是它们要么都满流，要么都不满流。

二、有源汇有上下界可行流

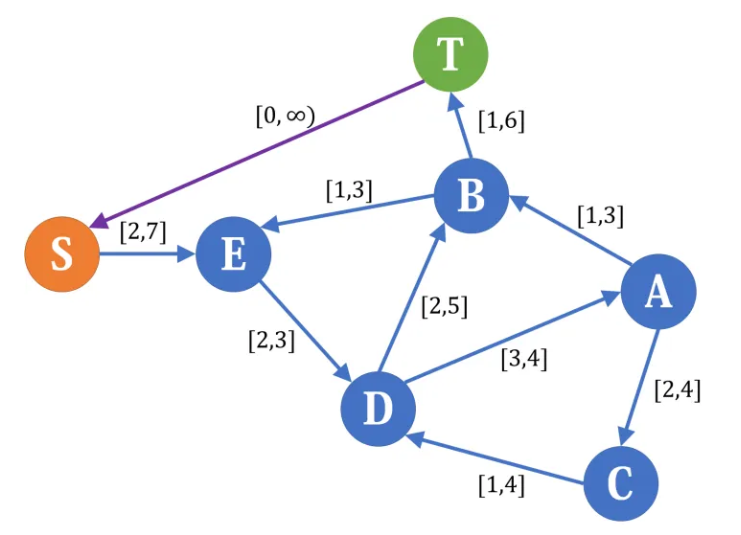
从汇点到源点连一条下界为0，上界为的附加边，得到一张和原图等价的无源汇流量网络，于是转化成了无源汇有上下界可行流问题。此时从源点到汇点的可行流流量，即为从汇点到源点的那条附加边的流量（注意下界网络中对应边流量为0）。

注意，这时候原来的源点和汇点已被处理成普通点，和之后差网络需要额外建立的源、汇点是不同的点，之后如果这两者同时出现，我们记前者为S、T，后者为S′、T′。

三、有源汇有上下界最大流

按照上一节的方法，我们已经得到了一个可行流，且知道它的流量就是T到S的附加边的流量。

要求从S到T的最大流，我们可以在差网络中把所有附加边删除，然后以S与T为源点与汇点，再求残余网络的最大流，加上可行流的流量即为原网络的最大流。这是因为，可行流已经保证了流量平衡，那么删去附加边后，我们再跑一次最大流把残余网络“榨干”，最后得到的流仍保证是平衡的。

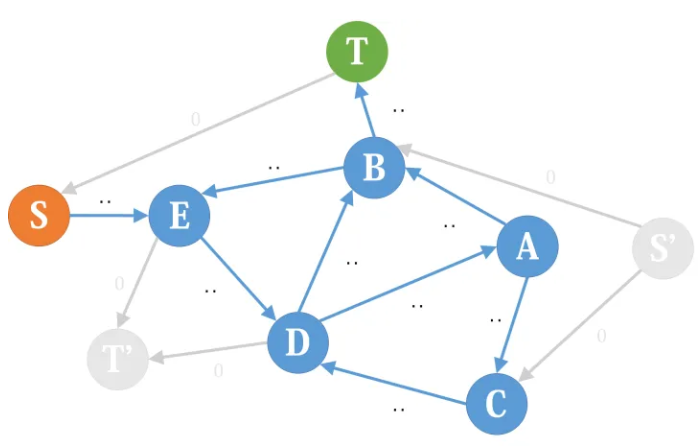
当然实际上S'与T'连接的附加边不需要删，这种出度或入度为0、又非源汇点的点是不影响最大流的，何况如果存在可行流，它们的残余容量已经为0了。