回溯法经典例题分析

点击打开在线编译器，边学边练

回溯法在我们解题步骤中经常被提到，这也是一种常用的方法，回溯法是一种经常被用在深度优先搜索（DFS）和广度优先搜索（BFS）的技巧。其本质是：走不通就回头。本篇将结合经典例题帮助大家对回溯法的理解。

一、工作原理：

（1）构造空间树；

（2）进行遍历；

（3）如遇到边界条件，即不再向下搜索，转而搜索另一条链；

（4）达到目标条件，输出结果。

二、经典例题

例题一：0-1背包问题

问题：给定n种物品和一背包。物品i的重量是wi，其价值为pi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

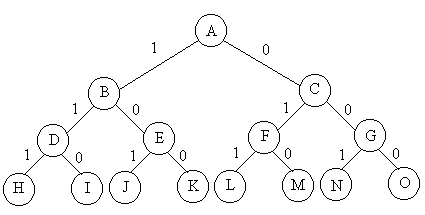
分析：问题是n个物品中选择部分物品，可知，问题的解空间是子集树。比如物品数目n=3时，其解空间树如下图，边为1代表选择该物品，边为0代表不选择该物品。使用x[i]表示物品i是否放入背包，x[i]=0表示不放，x[i]=1表示放入。回溯搜索过程，如果来到了叶子节点，表示一条搜索路径结束，如果该路径上存在更优的解，则保存下来。如果不是叶子节点，是中点的节点（如B），就遍历其子节点（D和E），如果子节点满足剪枝条件，就继续回溯搜索子节点。

0-1背包问题

代码如下：

#include <stdio.h>  
   
#define N 3         //物品的数量  
#define C 16        //背包的容量  
   
int w[N]={10,8,5};  //每个物品的重量  
int v[N]={5,4,1};   //每个物品的价值  
int x[N]={0,0,0};   //x[i]=1代表物品i放入背包，0代表不放入  
   
int CurWeight = 0;  //当前放入背包的物品总重量  
int CurValue = 0;   //当前放入背包的物品总价值  
   
int BestValue = 0;  //最优值；当前的最大价值，初始化为0  
int BestX[N];       //最优解；BestX[i]=1代表物品i放入背包，0代表不放入  
   
//t = 0 to N-1  
void backtrack(int t)  
{  
    //叶子节点，输出结果  
    if(t>N-1)   
    {  
        //如果找到了一个更优的解  
        if(CurValue>BestValue)  
        {  
            //保存更优的值和解  
            BestValue = CurValue;  
            for(int i=0;i<N;++i) BestX[i] = x[i];  
        }  
    }  
    else  
    {  
        //遍历当前节点的子节点：0 不放入背包，1放入背包  
        for(int i=0;i<=1;++i)  
        {  
            x[t]=i;  
   
            if(i==0) //不放入背包  
            {  
                backtrack(t+1);  
            }  
            else //放入背包  
            {  
                 //约束条件：放的下  
                if((CurWeight+w[t])<=C)  
                {  
                    CurWeight += w[t];  
                    CurValue += v[t];  
                    backtrack(t+1);  
                    CurWeight -= w[t];  
                    CurValue -= v[t];  
                }  
            }  
        }  
        //PS:上述代码为了更符合递归回溯的范式，并不够简洁  
    }  
}  
   
int main(int argc, char* argv[])  
{  
    backtrack(0);  
   
    printf("最优值：%d\n",BestValue);  
   
    for(int i=0;i<N;i++)  
    {  
       printf("最优解：%-3d",BestX[i]);  
    }  
    return 0;  
}

例题二：描述N皇后问题

问题：在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

N皇后问题等价于在n×n格的棋盘上放置n个皇后，任何2个皇后不放在同一行或同一列或同一斜线上。

分析：从n×n个格子中选择n个格子摆放皇后。可见解空间树为子集树。

使用Board[N][N]来表示棋盘，Board[i][j]=0 表示(I,j)位置为空，Board[i][j]=1 表示(I,j)位置摆放有一个皇后。

全局变量way表示总共的摆放方法数目。

使用Queen(t)来摆放第t个皇后。Queen(t) 函数符合子集树时的递归回溯范式。当t>N时，说明所有皇后都已经摆放完成，这是一个可行的摆放方法，输出结果；否则，遍历棋盘，找皇后t所有可行的摆放位置，Feasible(i,j) 判断皇后t能否摆放在位置(i,j)处，如果可以摆放则继续递归摆放皇后t+1，如果不能摆放，则判断下一个位置。

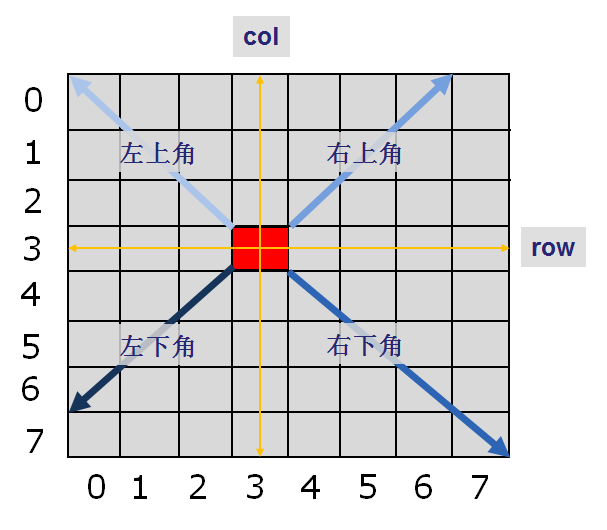
Feasible(row,col)函数首先判断位置(row,col)是否合法，继而判断(row,col)处是否已有皇后，有则冲突，返回0，无则继续判断行、列、斜方向是否冲突。斜方向分为左上角、左下角、右上角、右下角四个方向，每次从（row,col）向四个方向延伸一个格子，判断是否冲突。如果所有方向都没有冲突，则返回1，表示此位置可以摆放一个皇后。

描述N皇后问题

代码如下：

#include <stdio.h>  
   
#define N 8  
   
int Board[N][N];//棋盘 0表示空白 1表示有皇后  
int way;//摆放的方法数  
   
   
//判断能否在(x,y)的位置摆放一个皇后；0不可以，1可以  
int Feasible(int row,int col)  
{  
    //位置不合法  
    if(row>N || row<0 || col >N || col<0)  
        return 0;  
   
    //该位置已经有皇后了，不能  
    if(Board[row][col] != 0)  
    {   //在行列冲突判断中也包含了该判断，单独提出来为了提高效率  
        return 0;  
    }  
   
    //  
    //下面判断是否和已有的冲突  
   
    //行和列是否冲突  
    for(int i=0;i<N;++i)  
    {  
        if(Board[row][i] != 0 || Board[i][col]!=0)  
            return 0;  
    }  
   
    //斜线方向冲突  
   
    for(int i=1;i<N;++i)  
    {  
/* i表示从当前点(row,col)向四个斜方向扩展的长度 
  
左上角 \  / 右上角   i=2 
        \/           i=1 
        /\           i=1 
左下角 /  \ 右下角   i=2 
*/  
        //左上角  
        if((row-i)>=0 && (col-i)>=0)    //位置合法  
        {  
            if(Board[row-i][col-i] != 0)//此处已有皇后，冲突  
                return 0;  
        }  
   
        //左下角  
        if((row+i)<N && (col-i)>=0)  
        {  
            if(Board[row+i][col-i] != 0)  
                return 0;  
        }  
   
        //右上角  
        if((row-i)>=0 && (col+i)<N)  
        {  
            if(Board[row-i][col+i] != 0)  
                return 0;  
        }  
   
        //右下角  
        if((row+i)<N && (col+i)<N)  
        {  
            if(Board[row+i][col+i] != 0)  
                return 0;  
        }  
    }  
   
    return 1; //不会发生冲突，返回1  
}  
   
   
//摆放第t个皇后 ；从1开始  
void Queen(int t)  
{  
    //摆放完成，输出结果  
    if(t>N)  
    {  
        way++;  
        /*如果N较大，输出结果会很慢；N较小时，可以用下面代码输出结果 
        for(int i=0;i<N;++i){ 
            for(int j=0;j<N;++j) 
                printf("%-3d",Board[i][j]); 
            printf("\n"); 
        } 
        printf("\n------------------------\n\n"); 
        */  
    }  
    else  
    {  
        for(int i=0;i<N;++i)  
        {  
            for(int j=0;j<N;++j)  
            {  
                //（i,j）位置可以摆放皇后，不冲突  
                if(Feasible(i,j))  
                {  
                    Board[i][j] = 1;  //摆放皇后t  
                    Queen(t+1);       //递归摆放皇后t+1  
                    Board[i][j] = 0;  //恢复  
                }  
            }  
        }  
    }  
}  
   
//返回num的阶乘,num!  
int factorial(int num)  
{  
    if(num==0 || num==1)  
        return 1;  
    return num*factorial(num-1);  
}  
   
   
int main(int argc, char* argv[])  
{  
    //初始化  
    for(int i=0;i<N;++i)  
    {  
        for(int j=0;j<N;++j)  
        {  
            Board[i][j]=0;  
        }  
    }  
   
    way = 0;  
   
    Queen(1);  //从第1个皇后开始摆放  
   
    //如果每个皇后都不同  
    printf("考虑每个皇后都不同，摆放方法：%d\n",way);//N=8时, way=3709440 种  
   
    //如果每个皇后都一样，那么需要除以 N！出去重复的答案（因为相同，则每个皇后可任意调换位置）  
    printf("考虑每个皇后都不同，摆放方法：%d\n",way/factorial(N));//N=8时, way=3709440/8! = 92种  
   
    return 0;  
}

PS：该问题还有更优的解法。充分利用问题隐藏的约束条件：每个皇后必然在不同的行(列)，每个行(列)必然也只有一个皇后。这样我们就可以把N个皇后放到N个行中，使用Pos[i]表示皇后i在i行中的位置（也就是列号）（i = 0 to N-1）。这样代码会大大的简洁，因为节点的子节点数目会减少，判断冲突也更简单。

作业：