LGV引理可以用于在DAG上求解不相交路径方案数问题，下面我们简单介绍一下。
一、简介
LGV引理英文全称是Lindström–Gessel–Viennot lemma，可以用来处理有向无环图上不相交路径计数等问题。在此之前，大家要先了解图论相关概念、矩阵、高斯消元求行列式等知识，能帮助大家更快理解和学习LGV引理。
LGV 引理仅适用于有向无环图。
二、定义
ω(P) 表示P这条路径上所有边的边权之积。（路径计数时，可以将边权都设为 1）（事实上，边权可以为生成函数）
e(u,v)表示u到v的每一条路径P上的ω(P)值之和，即
起点集合A，是有向无环图点集的一个子集，大小为 n。
终点集合B，也是有向无环图点集的一个子集，大小也为 n。
一组A→B的不相交路径S：
是一条从
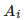到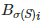
的路径（σ(S)是一个排列），对于任何
，
和
没有公共顶点。
N(σ)表示排列 σ 的逆序对个数。
三、引理
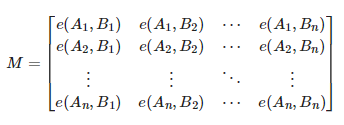
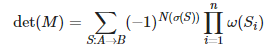
其中
表示满足上文要求的A→B的每一组不相交路径 S。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程，并配有习题和答疑，点击了解：
一点编程也不会写的：零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码？手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程：算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程