在图论中,如果一个有向图从任意顶点出发无法经过若干条边回到该点,则这个图是一个有向无环图(DAG图)。 因为有向图中一个点经过两种路线到达另一个点未必形成环,因此有向无环图未必能转化成树,但任何有向树均为有向无环图。
一、简介
有向无环图是图论的重要概念,我们将首先介绍图的概念和定义,随后介绍有向图,再逐渐引至有向无环图(DAG)。值得一提的是,当DAG用于指代模型时一般指向贝叶斯网络。
一个图G是顶点V的有限集合以及边E的多重集(每个连接两个不一定不同的顶点),在这里我们表示为G=V∪E,即V和E的并集,而没有写作其一般表示G=( V, E)。 图G=V∪E的大小由|E|表示的边缘(edge)确定, G的顺序是用|V|表示的顶点数。 下图给出了一些简单的示例:
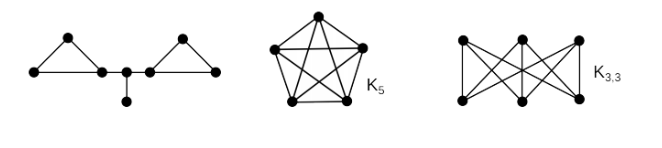
而有向图(diagraph)D是一组顶点V,连同弧(arc)的多重集A表示的,写作D=V∪A。
弧被表示为有序的顶点对,例如,a=(x,y),其中x是a的尾部,y是a的头部,而a则从尾部x到头部y。 A_v^+, A_v^- 分别表示从v出发或链接到v的集合。 因此我们可以用A_v = A_v^v ∪ A_v^- 来表示从v出发或链接到v的弧的集合。顶点v∈V的入边数量(in-degree)id(v)= d(v)^- 是 以v为头的弧。 类似地,对于任何v∈V,出边数量(out-degree) od(v)= d(v)^+是以v作为尾部的弧的数量。
对于每一个有向图,以下性质明显成立:
![]()
下图给出了一个具有弧a=(x,y),b=(y,x),...,的有向图示例。
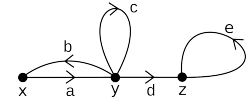
接下来我们需要引入环的概念。
我们定义开放路径(open trial)为一条没有顶点遍历多次(所有顶点都不相同)的路径。 在路径P(v_0,v_n)中,顶点v_1, ... , v_{n-1}被称为P(v_0,v_n)的内部顶点。 如果除了v_0 = v_n外,其他所有的顶点都不相同,并且它包含至少一个边,则我们称其为一个环,也即是闭合路径(closed trail)的定义。
下图给出了一些简单示例:
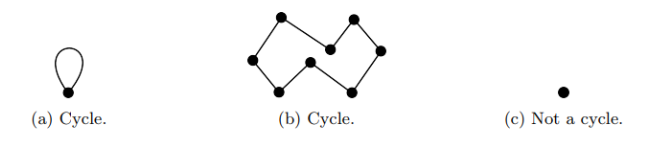
而一个图G或有向图D如果不包含(循)环(cycle),则称它为无环图(acyclic)。 一个无环图G被称为森林(forest),而只有一个组成部分的森林被称为树。
因此,我们可以很清晰的看到有向无环图(DAG)的定义为:有向无环图是没有环的有向图。
二、性质
1. 能拓扑排序的图,一定是有向无环图;如果有环,那么环上的任意两个节点在任意序列中都不满足条件了。
2. 有向无环图,一定能拓扑排序;(归纳法)假设节点数不超过 k 的 有向无环图都能拓扑排序,那么对于节点数等于 k 的,考虑执行拓扑排序第一步之后的情形即可。
三、判定
如何判定一个图是否是有向无环图呢?
检验它是否可以进行拓扑排序即可。当然也有另外的方法,可以对图进行一遍 DFS,在得到的 DFS 树上看看有没有连向祖先的非树边(返祖边)。如果有的话,那就有环了。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程