简述Pick定理

什么是皮克定理？

1899年，犹太数学家皮克（Georg Alexander Pick）发现了一个被誉为“有史以来最重要的100个数学定理之一”的“皮克定理”（Pick's Theorem）。这个定理是这样说的：给定顶点座标均是整点（或正方形格子点）的简单多边形，其面积?和内部格点数目?、边界格点数目?的关系为?=?+?/?−?。

例如：

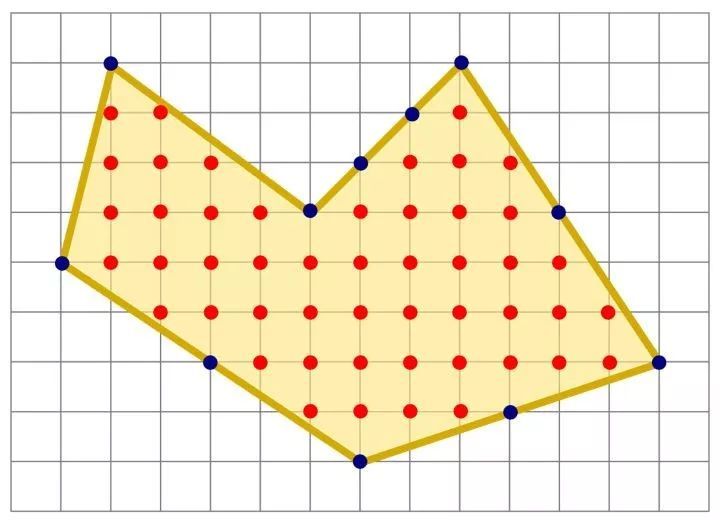
根据皮克定理，我们可以得到：

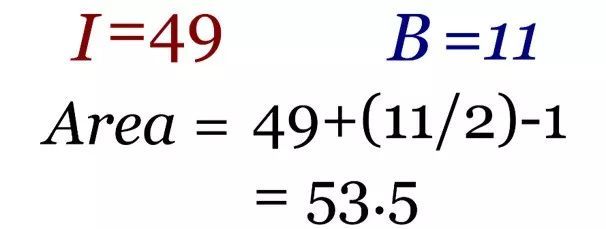
我们可以通过间接计算的方法验证这个结果：

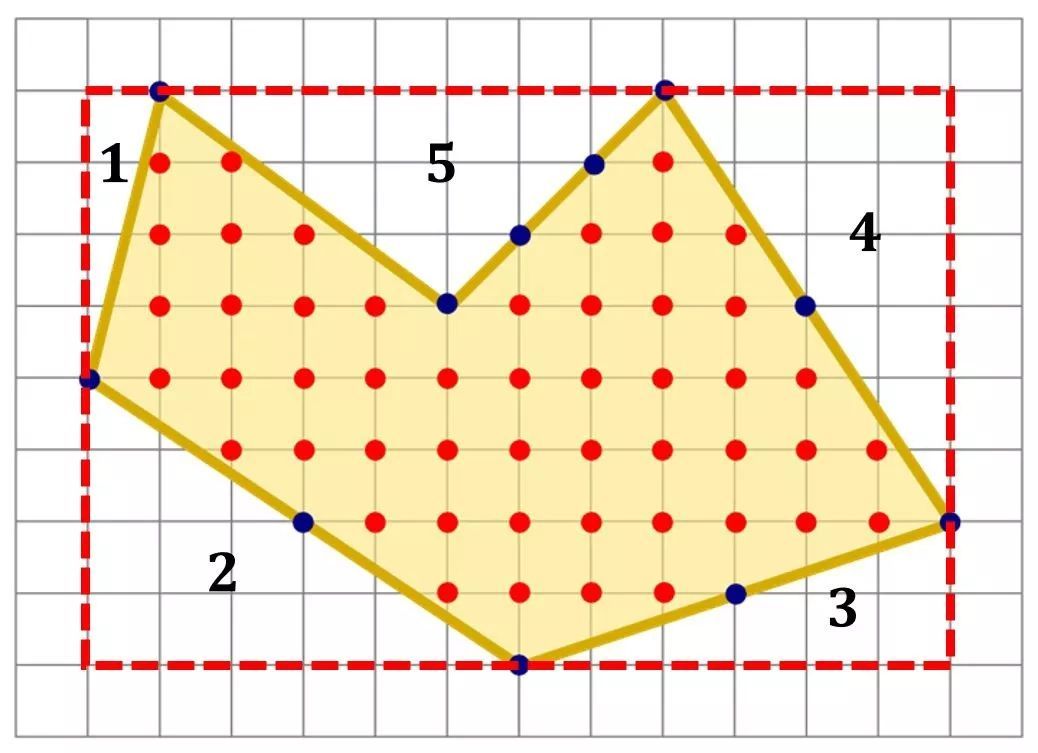
S＝S长方形－（S1＋S2＋S3＋S4＋S5）＝12×8－（1×4÷2＋6×4÷2＋6×2÷2＋6×4÷2＋7×3÷2）＝96－（2＋12＋6＋12＋10.5）＝96－42.5＝53.5。

最终的结果正如皮克定理所说的那样，面积的计算居然可以通过数点数来得到，很神奇对不对？

问题的起源

皮克定理的发现要从古埃及说起。

古埃及人铺地板时发现，用同样大小且同一种的正多边形铺地板时，只能用正三角形、正方形与正六边形，得到三种图案。

古埃及人又从铺地板中，发现三角形三个内角和为一平角（即180°）。

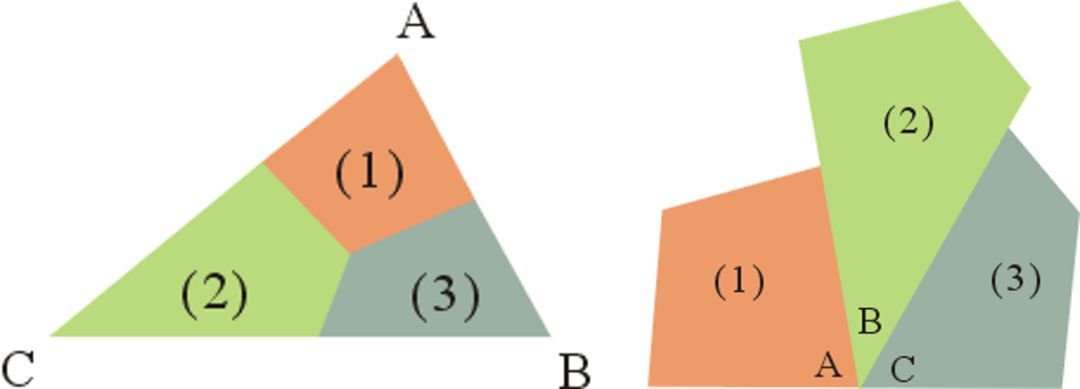
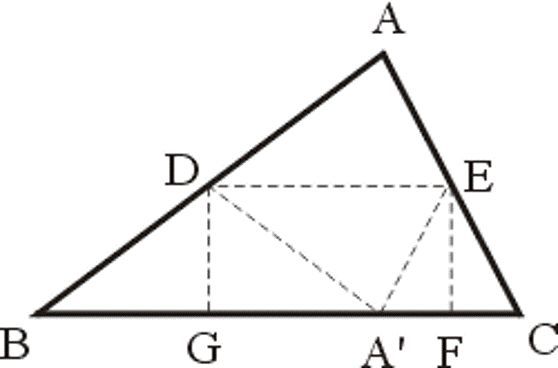
我们也可以利用折纸的实验，发现这个定理。即沿着DE、DG、EF把三角形折成长方形DEFG，那么∠?、∠?、∠?叠合于A’点，成为一个平角。

定理的证明

一般而言，数学是先有观察与猜测（这个阶段允许犯错），然后才有试验、修正与证明。数学绝不是突然从天上掉下一个公式或定理，然后就要我们去证明。

为了证明公式，首先让我们分析单纯多边形:

（1）最简单的单纯多边形就是原子三角形（atomic or primitive triangles），亦即除了三个顶点之外，三边及内部皆不含格子点之三角形，见下图，其面积皆为?/?，并且可用公式来计算：?/?+?−?=?/?。因此，对于原子三角形，上述公式成立。

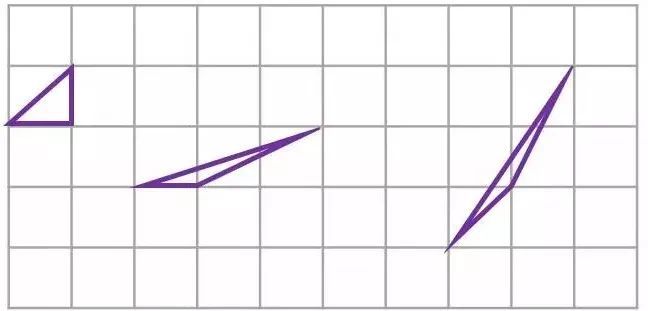
（2）其次，我们观察到对于任意的单纯多边形都可以先分割成三角形（即三角形化），再进一步分割成原子三角形的组合（这叫做原子化），见下图。

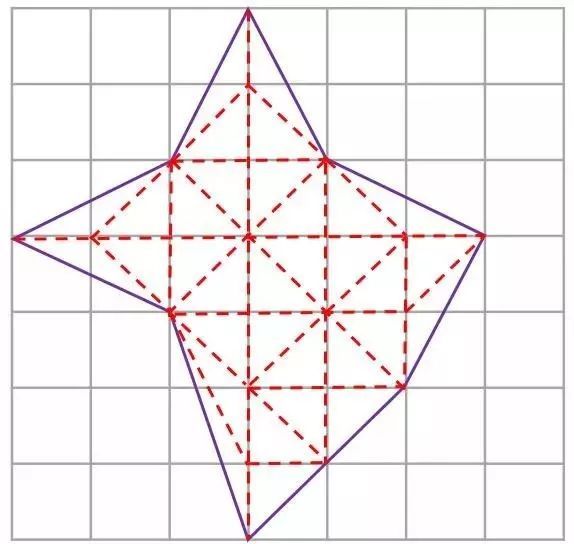
（3）最后考虑任何单纯多边形Γ，将它分割成两个单纯多边形Γ?与Γ?，见下图。设Γ有?个边界点、?个内点，并且Γ?和Γ?分别有??个与??个边界点、有??个与?2个内点。再设Γ?与Γ?有?3个共同的边界点。

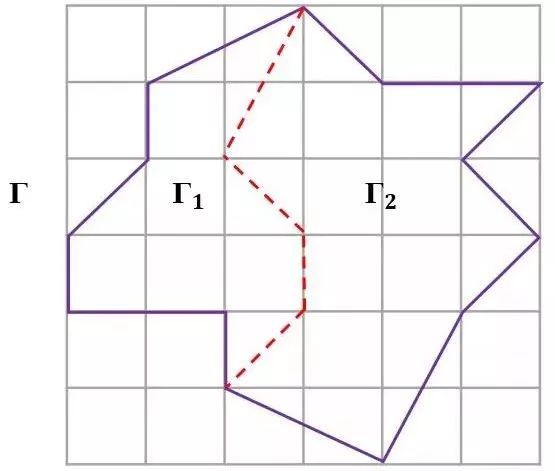
则：

?=??+??−???+?；?=??+??+??−?

所以：

?/?+?−?=(??/?+??−?)+(??/?+??−?)

即：Γ＝Γ?＋Γ?。

因此，我们发现，这个公式在分割下具有加性（additivity）。

现在换个角度再来证明一下这个定理的正确性。

重新整理皮克定理的证明思路，具体如下：

（1）首先，证明对长方形是成立的；

（2）接着，再证明对直角三角形是成立的；

（3）然后，继续证明对任意三角形也是成立的；

（4）最后，证明对于两个图形的组合还是成立的。

假设这个公式是对的，我们先看第四步：证明对于两个图形的组合是成立的。

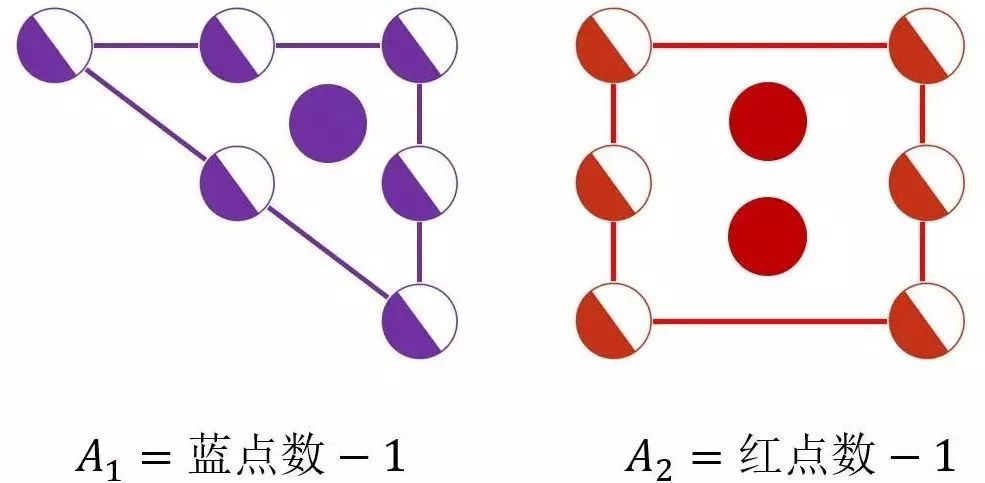
将两个图形组合在一起。注意：重合的两个边界点，分别多了1/2个点，所以最后是减去2，而不是减去1。

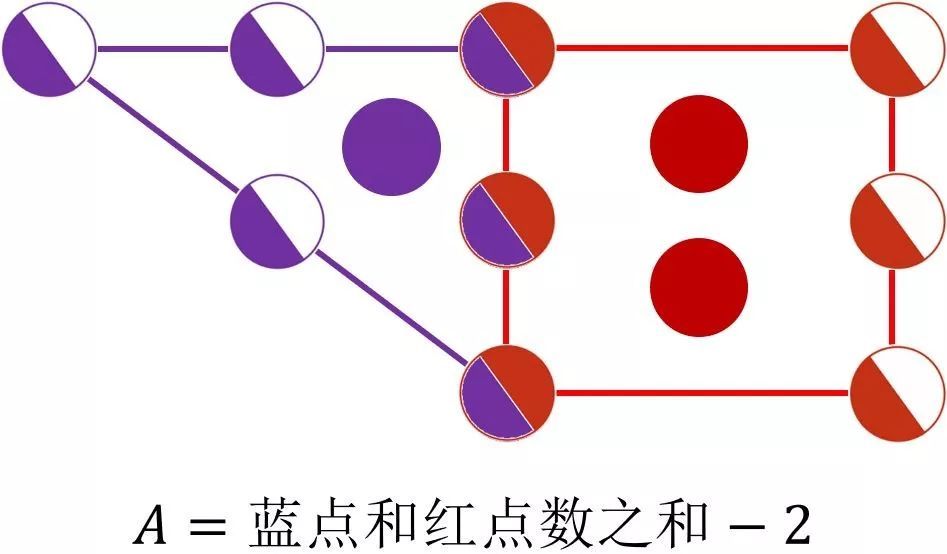
回头证明第一部分：公式对长方形是成立的。以一个长为?、宽为?的长方形为例。

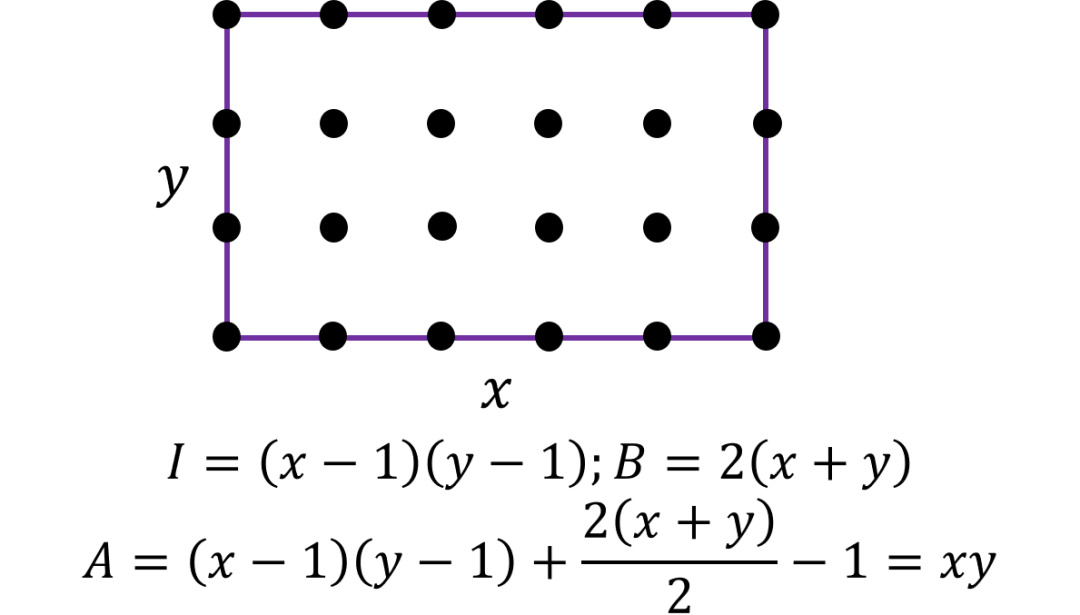
接着证明第二部分：对直角三角是成立的。以一个底为?、高为?的三角形为例。先假设斜边上没有边界点（除了顶点）。

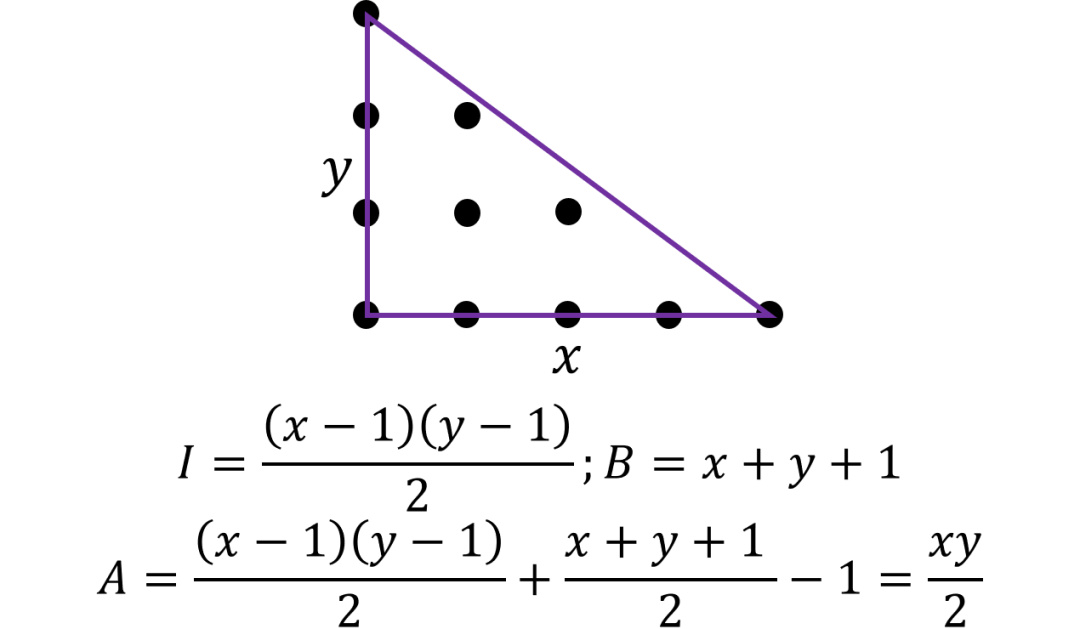
继续。现在考虑斜边上有边界点的情况。通过对第四种情况的证明，我们可以将三角形分割为长方形和三角形的组合。

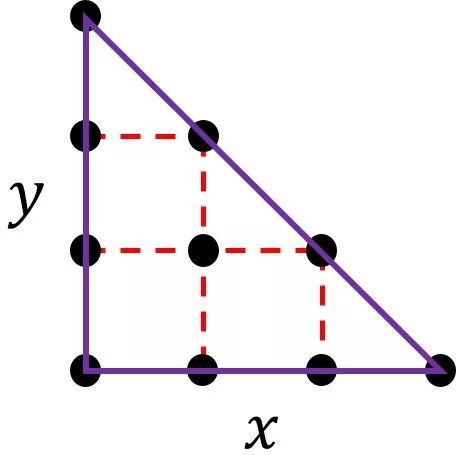
最后证明第三种情况：皮克定理对任意三角形也是成立的。

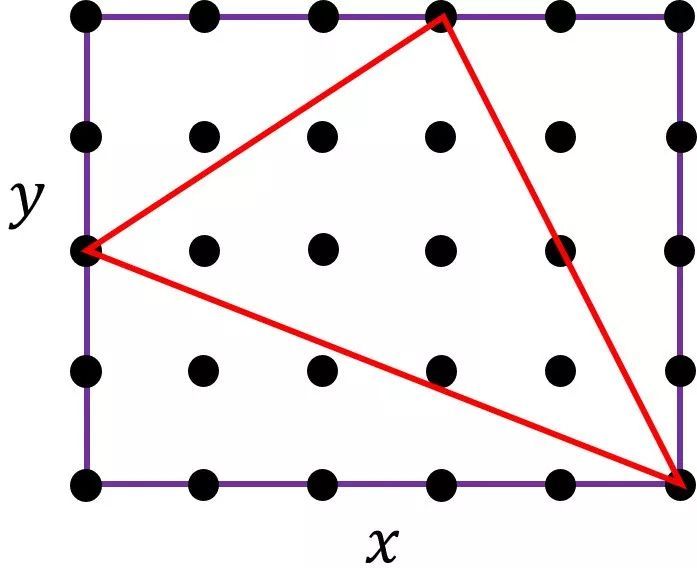
这里，我们可以通过从长方形减去外围三角形的方法得到证明。